《重学C++》6. C++基础句法

发表于 更新于 阅读次数： 本文字数： 2.7k 阅读时长 ≈ 2 分钟

1. 枚举enum

定义时类似于结构体：

1
2
3
4
enum wT{monday, tuesday, wednesday, thursday, friday, saturday, sunday};
wT week;
week = monday;
week = Tuesday;

枚举变量可以给其他变量赋值，但其他变量不能赋值给枚举变量

1
2
3
int a = 1;
// week = a;   错误，其他变量不能赋值给枚举变量
a = week;

枚举变量内部其实是通过int整型数字实现的，内部的第一个变量默认为0（也可指定为某数字），之后依次加一。

1
2
3
week = wT(1);    //一定要转换类型才能赋值，这里转换为tuesday
week = wednesday;
cout<< week  <<endl;    //输出2，即wednesday

2. 联合体和结构体内存

联合体中的所有数据共用一块数据，因此联合体的大小是其中最大元素的大小。

而结构体的大小是其中所有数据的大小之和，但涉及到内存对齐的问题。32位机器中，每4Byte作为一个整体，元素即使小于4Byte也要单独占据这块空间（除非和其他变量共占）。
（为了节省空间，应该尽量把小的数据元素放到一起）

元素即使小于4Byte也要单独在其中存放
此外，结构体内存大小还应当是最大元素的整数倍。

面试题经常考到这部分内容。

结构体大小的计算
https://www.runoob.com/w3cnote/struct-size.html


2. 函数

函数是一段封装好的代码，便于复用。
可以去使用一些比较好的公开库函数，可以节省开发成本，提高效率。但是有些场合对软件要求比较高，此时使用库函数可能不够高效而不能满足要求。

函数重载overload

函数名和函数参数列表，共同构成了函数签名。函数签名用来区别重载的函数。基本支持函数重载的语言都需要进行name mangling。mangling的目的就是为了给重载的函数不同的签名，以避免调用时的二义性调用。

函数指针和返回指针的函数

详见《C++易混变量类型》

命名空间

有的时候函数除了名字相同，参数也相同，这种时候不能重载，应当通过namespace解决这个问题。
下面的代码使用命名空间定义了一个函数和一个变量。

1
2
3
4
5
6
7
namespace  lu
{
	bool test() {
		return 1;
	}
	int constNum = 2;
}

有两种方法使用命名空间：

1
2
3
4
5
6
7
方法一：只需要在名称前加上命名空间的名称和两个冒号，即
cout <<  lu::constNum << endl;
cout << ( lu::test() == 1 )<< endl;
方法二：
using namespace lu;
cout <<  constNum << endl;
cout << ( test() == 1 )<< endl;

在实际使用中，可能需要在.h头文件中声明、.cpp文件中定义命名空间，最后在另一个.cpp文件中使用命名空间。


3. 函数体hack过程

函数压栈

函数调用过程中，默认会从右向左，先压入后面的参数、再压入前面的参数。
VS默认采取了__cdecl的调用约定方式，从右向左传递参数。这也是为什么只能给右边的函数参数加默认参数。

调用约定（调用惯例）的参数传递顺序
1.从右到左依次入栈：__stdcall，__cdecl，__thiscall，__fastcall
2.从左到右依次入栈：__pascal

Snipaste_2021-02-24_15-43-46.png

先压入后面的参数、再压入前面的参数

4. 递归

递归是一种重要的编程思想：

  1. 很多重要的算法都包含递归的思想；
  2. 递归最大的缺陷：
    1. 空间上需要开辟大量的栈空间；
    2. 时间上可能需要有大量重复运算；

递归的优化：

  1. 尾递归：所有递归形式的调用都出现在函数的末尾；
  2. 使用循环替代；
  3. 使用动态规划，空间换时间；

下面以斐波那契数列为例，列举优化后的方法。

循环优化递归

这种方法是以循环代替递归调用函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int Fib(int n)
{
	if(n <2)
	{
		return n;
	}
	int n0 = 0,n1 = 1;
	int temp;
	for(int i = 2;i <= n;++i)
	{
		temp = n0;
		n0 = n1;
		n1 = temp+n1;
	}
	return n1;
}

动态规划

动态规划思路是将每个计算过的数值存储起来，后期如果需要可以直接拿出来，不需要再次计算（空间换时间）。

这里就是用一个数组存储各个斐波那契的数值。

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<assert.h>
int a[1000];	//全局数组
int Fib(int n)
{
	a[0] = 0;
	a[1] = 1;
	for(int i <=2;i <= n;++i)
	{
		a[i] = a[i-1]+a[i-2];
	}  
	return a[n];
}
assert(Fib(10)==55);

尾递归

尾递归：所有递归形式的调用都出现在函数的末尾，并且只能直接返回递归函数的值（不能有加法等运算）。

什么是尾递归？ - 龙枪的回答 - 知乎
https://www.zhihu.com/question/20761771/answer/106426743

1
2
3
4
5
6
//不是尾递归，因为存在加法
 return Fib(n-1}+Fib(n-2);
//return Fib(n-1}+2; 这种方式也不是尾递归

//是尾递归
return Fib(n-1,ret1,ret0+ret1);

优化后的代码：

1
2
3
4
5
6
7
8
9
10
int Fib(int n,int ret0,int ret1)
{
	if(n == 0)
	{
		return ret0;
	}else if(n == 1){
		return ret1;
	}
	return Fib(n-1,ret1,ret0+ret1);
}

尾递归每次只需要保存一个递归信息，普通的递归每次需要保存两个函数的递归信息。长此以往是一个很大的开销。

没有尾递归优化时的调用过程

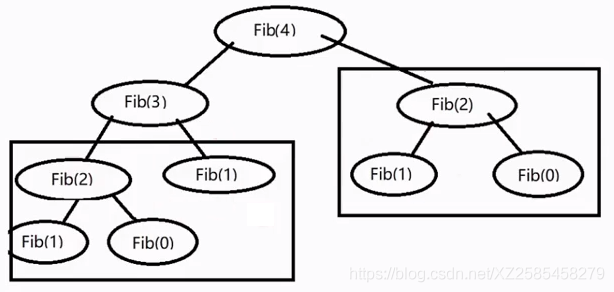
当有尾递归优化时，每次只调用一个递归函数，然后这个函数再向下调用一个（特点是直上直下、没有分支，类似于从头到尾访问一个链表）。这样的好处是，每次调用不会“分叉”，每轮永远只调用一个函数。从而节省了大量栈空间和重复计算的时间。

尾递归的优化：
在编译器中C/C+±>优化->优化->使大小最小化(/O1)
C/C+±>代码生成->基本运行时检查->默认值