Python培训Week6

发表于 更新于 阅读次数： 本文字数： 13k 阅读时长 ≈ 12 分钟

复习

对数据进行预处理的方式，注意预处理只改变X而不改变y：

  1. Rescale
  2. standardlize
  3. Normalize
  4. binarize

改进计算准确率accuracy score的方式：

  1. K-fold
    没有考虑到标签分组情况，还不够好
  2. StratifiedKFold

模型选择思路：

  1. 均值看准确率
  2. 标准差看稳定性

更直观的方式：

  1. 箱子图
  2. Confusion Matrix 混淆矩阵/模糊矩阵

今天主要有3个专题：

  1. 将训练好的模型持久化保存
  2. 从数据预处理到算法评估，搭建一整套框架完整这些任务
  3. 对数据进行降维处理

1.Finalize模型固化/持久化

根据数据选择出一个最合适的算法后，将数据、算法参数等存储起来进行Finalize。便于后面用户提供新数据后直接使用。算是Model Selection的Output。



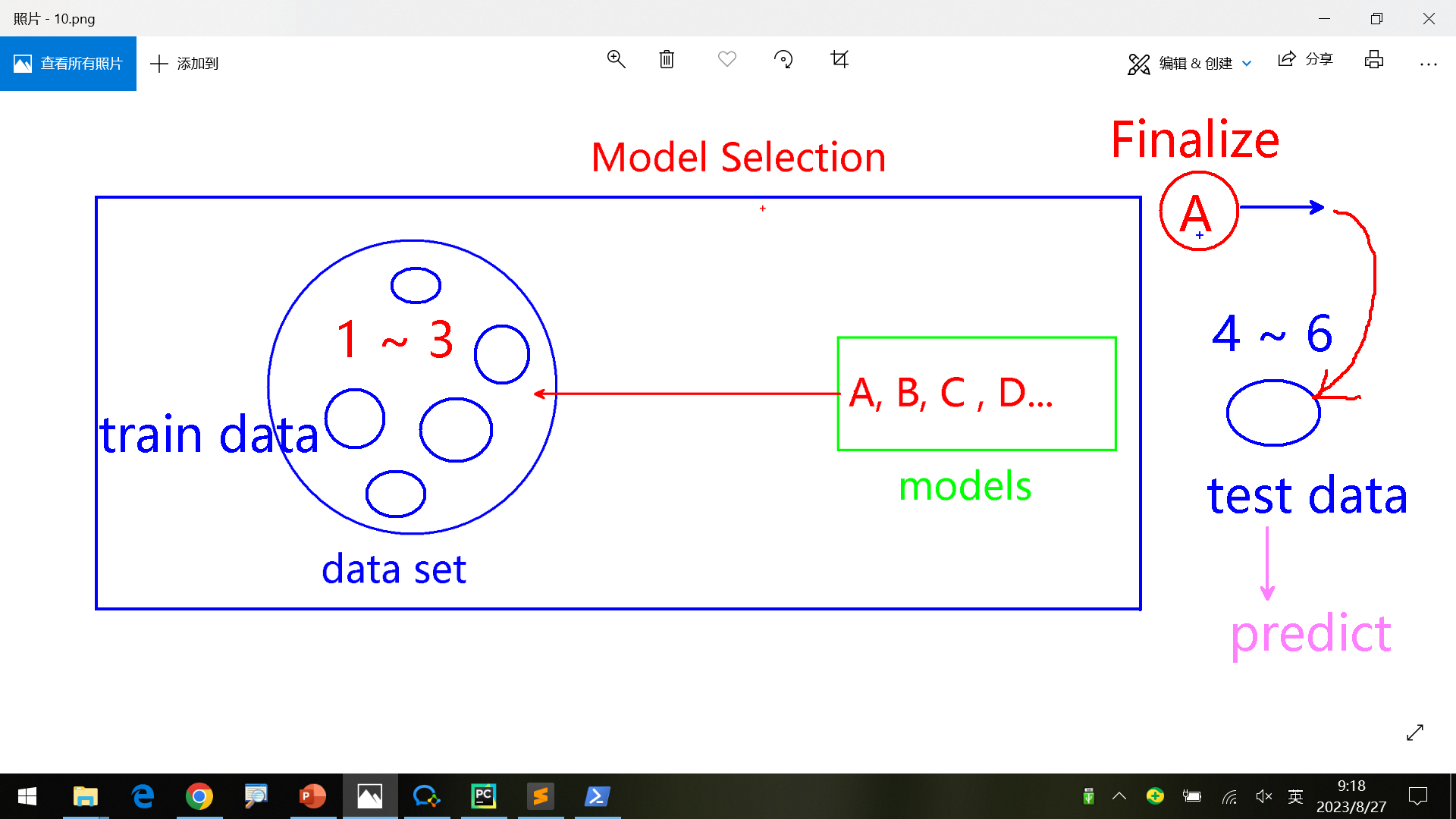
image.png

如何保存和使用？

流程是读取数据、使用算法最后训练一次、最后使用pickle将模型（数据和算法）保存。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import  pandas as pd  
from sklearn.linear_model import  LogisticRegression  
import  pickle  
  
data_set = pd.read_csv("../pima-indians-diabetes.csv")  
feature_columns = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age']  
X = data_set[feature_columns]  
y = data_set.label  
  
model = LogisticRegression(solver='liblinear')  
model.fit(X.values,y.values)  
  
# 前面是读入数据并进行最后的训练，下面是最后写入文件  
filename = '../Finalized model.ml'  
pickle.dump(model, open(filename,'wb'))

使用时再读入文件

1
2
3
4
5
6
7
8
9
import  pickle  
import numpy as np  
  
filename = "../Finalized model.ml"  
loaded_model = pickle.load(open(filename, 'rb'))  
  
test_data = [5, 116, 74, 0, 0, 25.6, 0.201, 30]  
y_pred = loaded_model.predict(np.array(test_data).reshape(1,-1))  
print(y_pred)

得到输出

[0]

为什么数据很重要？

单纯软件开发->没有数据积累，客户可以随时更换供应商；
软件开发+数据存储积累->除了软件，还可以根据数据提供相应数据分析报表，增加用户粘性；后期数据越多，数据分析越准确，而且客户要迁移可能还要买回数据，成本很高。



2.Framework(Model Selection)

每次数据分析的流程大致是:

  1. preprocessing
  2. model selection
  3. score
  4. …

可以将前3步做成pipeline的形式，简化重复劳动

另外还有DataGenerator, 在客户数据到来之前生成模拟数据



1.生成dataset

练习可以用sklearn.datasets的make_*方法，实际一般根据客户真实数据构造 

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.datasets import  make_classification  
  
def load_data_set():  
    # n_informative 是指有用、权重较高的数据  
    # n_redundant 是指冗余数据  
    # n_classes 分类的数量，有几种分类  
    X,y = make_classification(n_samples=1000, n_classes=2 )  
    return  X,y  
  
X,y = load_data_set()  
print(X)  
print(y)

输出如下：

[[-2.43850005 -0.07321394 0.91037513 … 0.17318305 -0.48545443
0.50529299]
[ 0.26199228 -0.63133888 -0.17787624 … -2.38110847 0.35979645
0.37771326]
[ 0.05085058 0.73357154 0.23160743 … -1.26857873 -2.0520035
0.97842607]
…
[ 0.03034656 0.23028396 -1.90049935 … -0.3695487 -1.75098982
0.13479775]
[-0.1134665 -0.34927547 0.57881782 … 2.05341675 -1.10515843
-1.46092126]
[-0.23639439 -0.4040107 -0.66023956 … 0.59499224 -0.53790146
-0.81610969]]
[1 1 0 0 1 1 1 1 0 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0
0 1 1 0 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 1 0 1 0 1 1 0 0 0 1 0 1 1 0 1 0 0 1
1 0 1 0 0 0 1 1 1 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 1 0 0 1 0 0 0 1 0 0 1 1 0
0 1 0 1 0 0 1 0 0 1 0 0 1 0 0 0 1 1 1 1 0 1 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0
1 0 1 1 1 0 0 0 1 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0
0 0 1 0 0 1 1 1 1 0 1 1 0 1 1 0 1 1 0 0 1 1 0 1 0 1 0 1 1 0 1 1 0 0 1 1 0
1 1 0 0 0 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0
0 0 1 0 1 1 1 0 1 1 0 0 1 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 1
1 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0
1 1 1 0 1 1 0 1 1 1 0 1 1 1 0 0 0 1 1 1 0 0 1 1 0 1 1 1 0 1 0 1 1 0 0 1 0
0 0 1 1 1 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 0 1 1 0 0 1 0 0
1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1
1 0 1 0 1 1 0 0 1 0 0 1 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 1 1 1 1 1 1 0 0 1
0 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 1 0 0 1 0 1
1 0 1 0 0 1 1 0 1 1 1 1 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 0 1 1
0 0 1 0 0 1 1 1 0 0 1 1 1 0 1 0 0 0 0 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 1 1 1
0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 1 1 1 1
0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1
1 0 1 1 0 0 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 1 1 0 1 0 1 0 1 0 1 1 1 0
1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 1
1 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 0 0 0 1 0 1
0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 0 1 0 0 1 1
1 1 0 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 1 1 0 0 1 0 0 0 0 1 1 1 1 0
0 1 0 0 0 0 1 1 1 1 1 0 0 0 1 0 0 1 0 0 0 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0
1 1 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 1
1 1 1 1 0 0 1 0 0 0 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 1 1 0
0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 1 0 1 1 1 1 0 1 1 1 1 0 0 1
1]

2.添加算法

首先需要添加/支持几种算法，这里用之前学过的几种

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.neighbors import  KNeighborsClassifier  
from sklearn.tree import DecisionTreeClassifier  
from sklearn.naive_bayes import GaussianNB  
from sklearn.svm import  SVC  
from sklearn.linear_model import  LogisticRegression  

def define_models():  
    models = dict()  
    models['KNN'] = KNeighborsClassifier()  
    models['DTC'] = DecisionTreeClassifier()  
    models['GNB'] = GaussianNB()  
    models['SVM'] = SVC()  
    models['LR'] = LogisticRegression()  
    return  models  
  

print(define_models())

输出：

{‘KNN’: KNeighborsClassifier(), ‘DTC’: DecisionTreeClassifier(), ‘GNB’: GaussianNB(), ‘SVM’: SVC(), ‘LR’: LogisticRegression()}

3.构建Pipeline

一个pipeline是一个处理的完整流程，这里包括标准化，正常化和算法评估。实际生产可以根据需要自定义步骤。 

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.preprocessing import StandardScaler  
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline

def make_pipeline(model):  
    # 执行每一步，然后执行下一步  
    # 这种pipeline在项目中使用更多，而不是之前的步骤  
    steps = list()  
    steps.append(('Standardize',StandardScaler()))  
    steps.append(('Normalize', MinMaxScaler()))  
    steps.append(('Model', model))  
    pipeline = Pipeline(steps= steps)  
    return  pipeline

对一个算法要执行pipeline中的所有步骤。
因此evaluate_single_model中执行pipeline，进行评估。 

1
2
3
4
5
6
7
8
from sklearn.model_selection import  KFold  
from sklearn.model_selection import cross_val_score

def evaluate_single_model(X, y, model, kfold):  
    # estimator可以是单个model，也可以是pipeline(多个模型每个处理一遍)  
    pipeline = make_pipeline(model)  
    cv_score = cross_val_score(pipeline, X, y, cv=kfold, scoring='accuracy')  
    return  cv_score

整合

结合之前的代码，得到最后的程序。
首先通过make_classification构建数据;
然后添加所有要评估的算法到字典models中;
接下来写出单个算法评估的流程：构建使用当前算法的pipeline，并使用它执行cross_val_score;
最后遍历models，写出对所有算法进行评估的代码。注意对异常情况的处理等。

最终代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
from sklearn.datasets import  make_classification  
  
from sklearn.neighbors import  KNeighborsClassifier  
  
from sklearn.tree import DecisionTreeClassifier  
from sklearn.naive_bayes import GaussianNB  
from sklearn.svm import  SVC  
from sklearn.linear_model import  LogisticRegression  
from sklearn.preprocessing import StandardScaler  
from sklearn.preprocessing import MinMaxScaler  
from sklearn.pipeline import Pipeline  
  
from sklearn.model_selection import  KFold  
from sklearn.model_selection import cross_val_score  
import  numpy as np  
  
def load_data_set():  
    # n_informative 是指有用、权重较高的数据  
    # n_redundant 是指冗余数据  
    # n_classes 分类的数量，有几种分类  
    X,y = make_classification(n_samples=1000, n_classes=2 )  
  
    return  X,y  
  
def define_models():  
    models = dict()  
    models['KNN'] = KNeighborsClassifier()  
    models['DTC'] = DecisionTreeClassifier()  
    models['GNB'] = GaussianNB()  
    models['SVM'] = SVC()  
    models['LR'] = LogisticRegression()  
  
    return  models  
  
def make_pipeline(model):  
    # 执行每一步，然后执行下一步  
    # 这种pipeline在项目中使用更多，而不是之前的步骤  
    steps = list()  
    steps.append(('Standardize',StandardScaler()))  
    steps.append(('Normalize', MinMaxScaler()))  
    steps.append(('Model', model))  
    pipeline = Pipeline(steps= steps)  
  
    return  pipeline  
  
def evaluate_single_model(X, y, model, kfold):  
    # cross_val_score的参数estimator可以是单个model，也可以是pipeline(多个模型每个处理一遍)  
    pipeline = make_pipeline(model)  
    cv_score = cross_val_score(pipeline, X, y, cv=kfold, scoring='accuracy')  
    return  cv_score  
  
def evaluate_models(X, y, models, kfold=10):  
    results = dict()  
    for name, model in models.items():  
        cv_score = evaluate_single_model(X,y,model, kfold)  
        results[name] = cv_score  
        if cv_score is not None:  
            mean_score, std_score = np.mean(cv_score), np.std(cv_score)  
            print("%s : %.3f (+/-%.3f)" %(name, mean_score, std_score))  
        else:  
            print("%s Error" % name)  


X,y = load_data_set()  
models = define_models()  
evaluate_models(X,y, models)

执行结果： 

1
2
3
4
5
KNN : 0.902 (+/-0.029)
DTC : 0.899 (+/-0.018)
GNB : 0.919 (+/-0.025)
SVM : 0.926 (+/-0.021)
LR : 0.925 (+/-0.022)

3.Dimensionality Reduction降维

前面都完成之后，进一步优化。如何在准确度不降低的情况下，如何提高性能？
PCA算法 Principal component analysis
主元分析法，降维是对数据整体做缩放而不是真正把数据减少了，降维后不叫“维(dimension)”叫做“元(component)”



比如原来纬度=8，太小会影响正确率，太大效果不明显，如何确定降维到多少？(feature selection)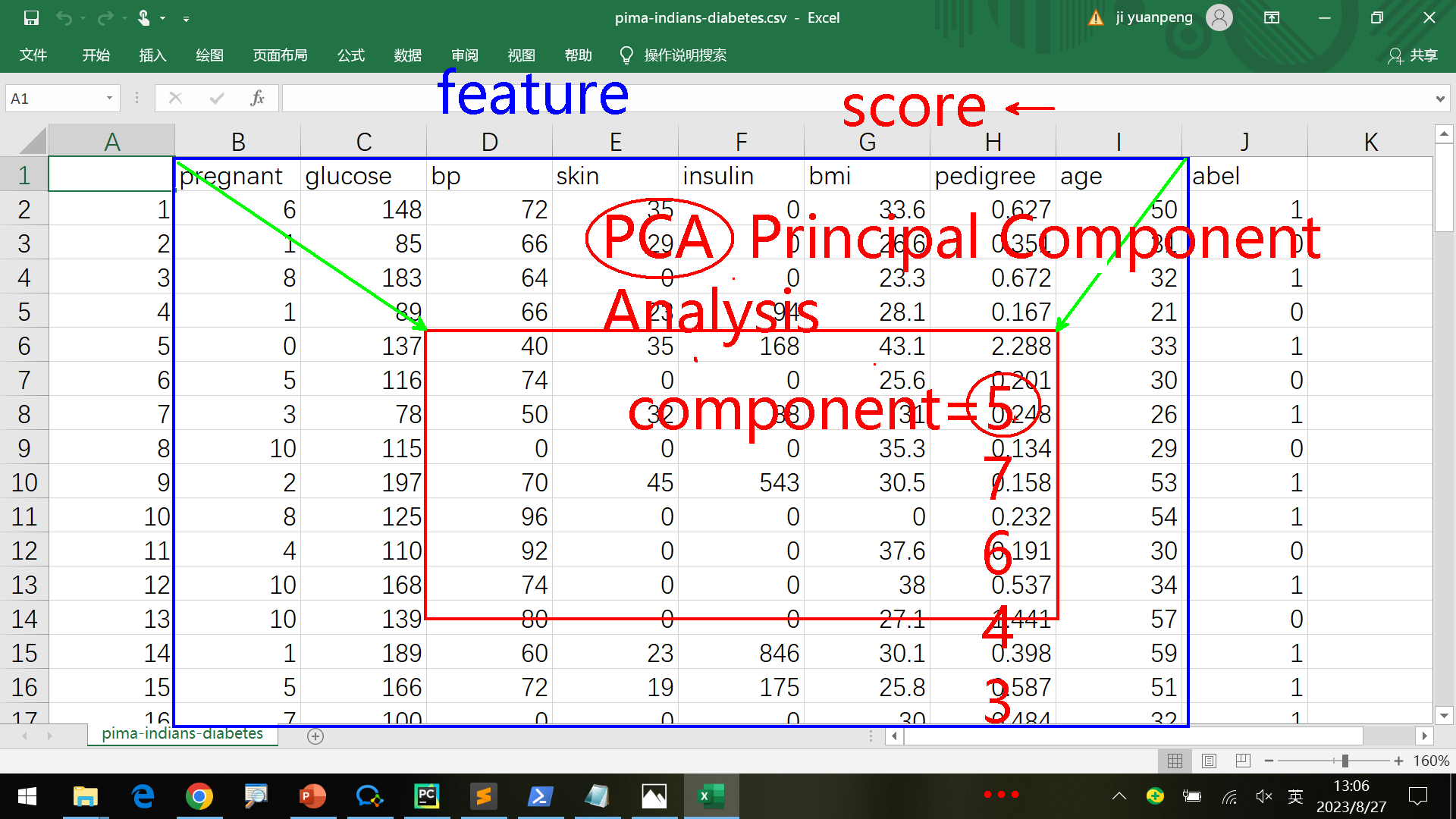
image.png

如何降维

可以使用sklearn.decomposition.PCA算法，简单的降维样例如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.datasets import  make_classification  
from sklearn.decomposition import  PCA  
  
  
def load_data_set():  
    X,y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5)  
    return  X,y  
  
def dimensionality_reduction(X,y):  
    pca = PCA(n_components=5)  
    X_new = pca.fit_transform(X,y) # y只为了参考，降维只针对X  
    return  X_new  
  
if __name__== '__main__':  
    X,y = load_data_set()  
    X_new = dimensionality_reduction(X,y)  
    print(X_new)

输出如下

[[ 7.59493044 0.98974276 -12.51113226 11.15523235 -6.955298 ]
[ -9.93846815 4.81754693 -4.11132752 1.45977825 5.09960183]
[ -4.02382826 9.14378059 -0.66566083 8.4283571 -4.53549432]
…
[ -2.4894288 1.14399821 0.79507779 0.23280763 6.41014444]
[-11.87515806 1.99982065 9.13962293 -11.89488371 -4.99407061]
[ 4.43287365 -5.00665058 2.28123668 -2.98325281 5.11717823]]

模型

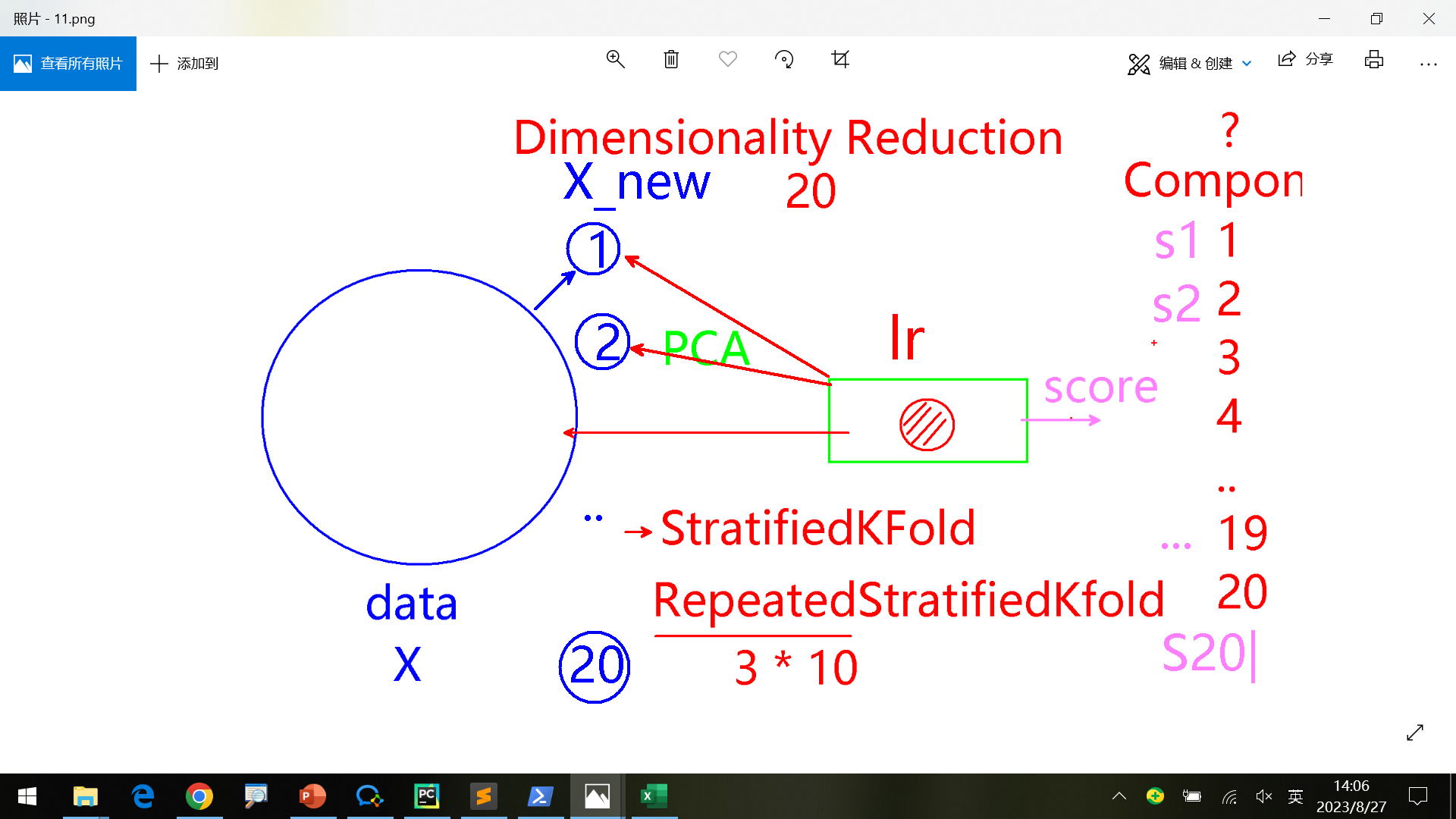
image.png

思路
使用同样的算法、对降维后不同纬度的数据计算准确率，从而选出最适合的纬度。
第1次计算数据纬度=1的准确率
第2次计算数据纬度=2的准确率
…
第n次计算数据纬度=n的准确率（相当于没有降维）

准确率计算
之前使用KFold, StratifiedKFold。但这两种在降维方面很难显示出差异，因为各纬度准确度差别很小。
可以使用RepeatedStratifiedKFold（比如每轮10次, 3轮，那么一共是从3*10个数据中得到最后的数据）

以降维到15为例，初步的代码如下：
n_features是属性的总数，n_informative是指有意义的属性的数量，n_redundant是冗余属性的数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from sklearn.datasets import  make_classification  
from sklearn.decomposition import  PCA  
from sklearn.linear_model import LogisticRegression  
from sklearn.model_selection import RepeatedStratifiedKFold  
from sklearn.model_selection import cross_val_score  
  
def load_data_set():  
    X,y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5)  
    return  X,y  
  
def dimensionality_reduction(X,y=None):  
    pca = PCA(n_components=15)  
    X_new = pca.fit_transform(X,y) # y只为了参考，降维只针对X  
    return  X_new  
  
def define_model():  
    return LogisticRegression()  
  
def evaluate_model(X,y,model):  
    kfold = RepeatedStratifiedKFold(n_splits=10, n_repeats=3)  
    cv_score = cross_val_score(model, X, y, cv=kfold, scoring='accuracy')  
  
    return  cv_score  
  
if __name__== '__main__':  
    X,y = load_data_set()  
    X_new = dimensionality_reduction(X,y)  
    model = define_model()  
    cv_score = evaluate_model(X_new, y, model)  
    print(cv_score.mean(), cv_score.std())

输出：

0.8580000000000001 0.03994996871087636

但是模型还不够好，需要人工干预。可以继续优化。

优化

主要修改dimensionality_reduction和define_model，原来这2部分之前需要手动改。
将define_model和dimensionality_reduction结合，修改为返回一个pipeline数组，每个pipeline执行2个步骤，分别是：pca和算法部分。最后修改调用部分，对每个pipeline调用evaluate_model进行评估，并打印数据。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from sklearn.datasets import  make_classification  
from sklearn.decomposition import  PCA  
from sklearn.linear_model import LogisticRegression  
from sklearn.model_selection import RepeatedStratifiedKFold  
from sklearn.model_selection import cross_val_score  
from sklearn.pipeline import Pipeline  
import  matplotlib.pyplot as plt  
  
def load_data_set():  
    X,y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5)  
    return  X,y  
  
# def dimensionality_reduction(X,y=None):  
#     pca = PCA(n_components=15)  
#     X_new = pca.fit_transform(X,y) # y只为了参考，降维只针对X  
#     return  X_new  
  
def define_model():  
    models = dict()  
    for i in range(1, 21):  
        steps = [('pca', PCA(n_components=i)),  
                 ('model', LogisticRegression())] # 如果步骤比较少可以这么写，如果多可以写申请list然后append每一步  
        pipeline = Pipeline(steps = steps)  
        models[i] = pipeline  
    return models  
  
def evaluate_model(X,y,model):  
    kfold = RepeatedStratifiedKFold(n_splits=10, n_repeats=3)  
    cv_score = cross_val_score(model, X, y, cv=kfold, scoring='accuracy')  
  
    return  cv_score  
  
if __name__== '__main__':  
    X,y = load_data_set()  
    # X_new = dimensionality_reduction(X,y)  
    models = define_model()  
    names = []  
    results = []  
    for name, model in models.items():  
        cv_score = evaluate_model(X, y, model)  
        names.append(name)  
        results.append(cv_score)  
        print('%s : %f' % (name, cv_score.mean()) )  
    plt.boxplot(results, labels=names)  
    plt.show()

最后还可以使用boxplot分析数据，更直观地查看各元时的准确率。
如下图，均衡考虑到低维和高准确率，降维到15是最合适的。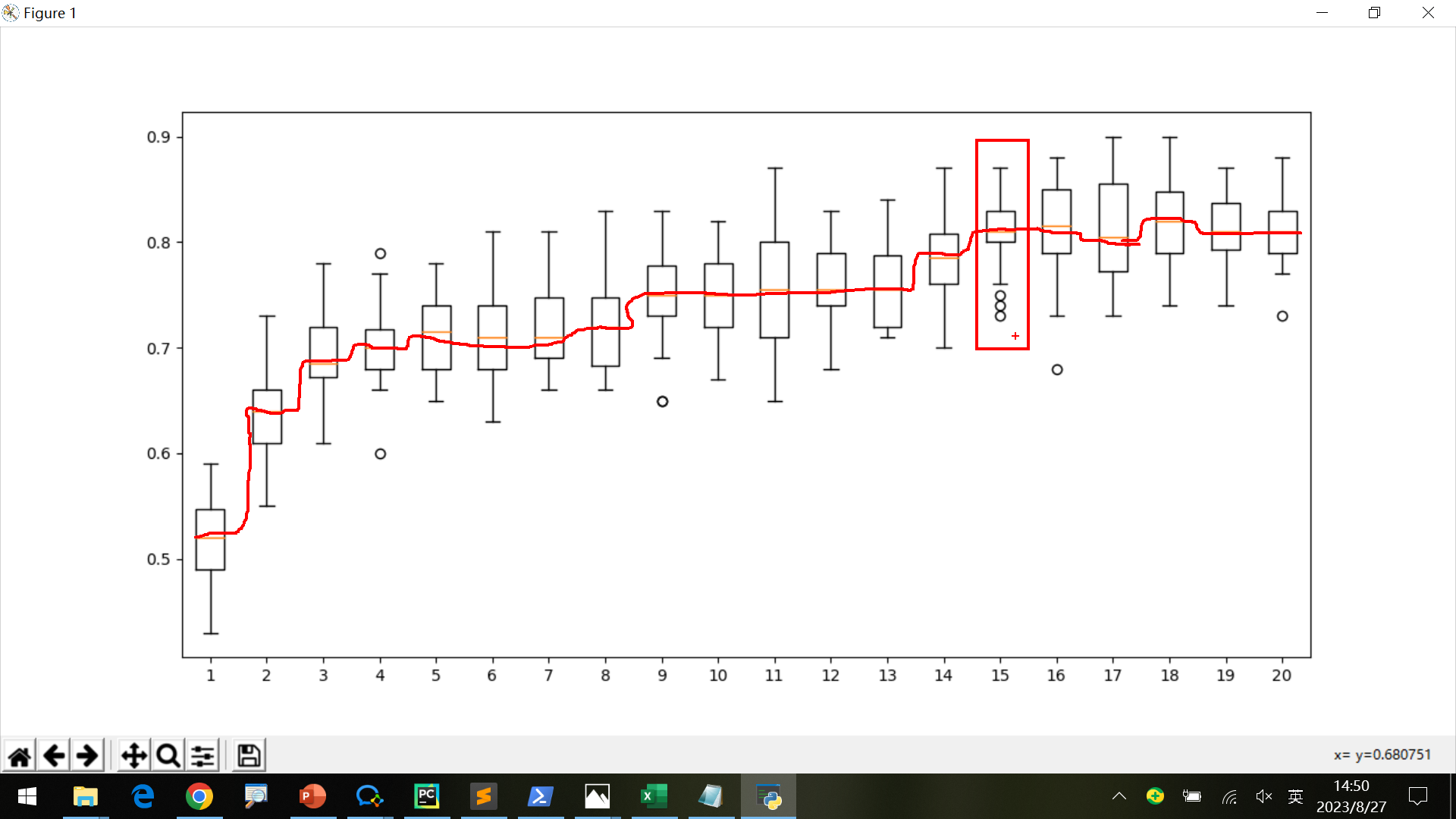
image.png

4.frequent item set常用物品组合

使用apriori算法。将数据类似预处理组成新矩阵后，作为算法输入。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from mlxtend.frequent_patterns import apriori  
from mlxtend.preprocessing import TransactionEncoder  
import  pandas as pd  
  
  
data_set = [['Apple', 'Beer', 'Rice', 'Chicken'],  
             ['Apple', 'Beer', 'Rice'],  
             ['Apple', 'Beer'],  
             ['Apple', 'Bananas'],  
             ['Milk', 'Beer', 'Rice', 'Chicken'],  
             ['Milk', 'Beer', 'Rice'],  
             ['Milk', 'Beer'],  
             ['Apple', 'Bananas']]  
  
  
te = TransactionEncoder()  
data_set_new = te.fit_transform(data_set)  
print(te.columns_)  
print(data_set_new)  
  
df = pd.DataFrame(data_set_new, columns= te.columns_)  
  
frequent_item_set = apriori(df, use_colnames=True)  
print(frequent_item_set)

输出结果:

[‘Apple’, ‘Bananas’, ‘Beer’, ‘Chicken’, ‘Milk’, ‘Rice’]
[[ True False True True False True]
[ True False True False False True]
[ True False True False False False]
[ True True False False False False]
[False False True True True True]
[False False True False True True]
[False False True False True False]
[ True True False False False False]]
support itemsets
0 0.625 (Apple)
1 0.750 (Beer)
2 0.500 (Rice)
3 0.500 (Beer, Rice)

其他

不要拷贝程序

直接拷贝程序学不到东西，还经常需要修改
最好分析思路，再用代码语言写出这种逻辑

读取csv文件列名

像之前糖尿病的csv文件，不是必须写出列名读取。
比如像字母识别的文件，格式如下，可以看出第一列是label，其他是features：

lettr,x-box,y-box,width,high,onpix,x-bar,y-bar,x2bar,y2bar,xybar,x2ybr,xy2br,x-ege,xegvy,y-ege,yegvx
T,2,8,3,5,1,8,13,0,6,6,10,8,0,8,0,8
…

可以按照列名和下标读取：

1
2
3
4
5
6
7
import pandas as pd  
  
data_set = pd.read_csv("../letter-recognition.csv")   #文件名  
X = data_set[1:]  
y = data_set.lettr  
  
print(X,y)

输出如下：

lettr x-box y-box width high … xy2br x-ege xegvy y-ege yegvx
1 I 5 12 3 7 … 9 2 8 4 10
2 D 4 11 6 8 … 7 3 7 3 9
3 N 7 11 6 6 … 10 6 10 2 8
4 G 2 1 3 1 … 9 1 7 5 10
5 S 4 11 5 8 … 6 0 8 9 7
… … … … … … … … … … … …
19995 D 2 2 3 3 … 4 2 8 3 7
19996 C 7 10 8 8 … 13 2 9 3 7
19997 T 6 9 6 7 … 5 2 12 2 4
19998 S 2 3 4 2 … 8 1 9 5 8
19999 A 4 9 6 6 … 8 2 7 2 8

[19999 rows x 17 columns] 0 T
1 I
2 D
3 N
4 G
..
19995 D
19996 C
19997 T
19998 S
19999 A
Name: lettr, Length: 20000, dtype: object

不要做低层次的岗位

一线人员，二线人员……最高层的人员在实验室，平时喝喝咖啡、学习思考，不出面，只做一些思考的工作。
一线的人反而天天各地跑，甚至晚上工作。