Python培训Week7

发表于 更新于 阅读次数： 本文字数： 16k 阅读时长 ≈ 14 分钟

复习

  1. Finalize持久化，将算法、参数和数据持久化为一个文件
  2. Framework框架，将模型选择的总体流程打包为一个框架
    pipeline管道方式
  3. Dimensionality Reduction降维
    降维使用 PCA 主元分析法，pipeline管道方式作为流水线
  4. frequent item set常用物品组合

今天的内容主要是算法的详细深入讲解，不再是简单调用第三方库，而是完全自己实现用到的算法，这才是真正工作中的场景。

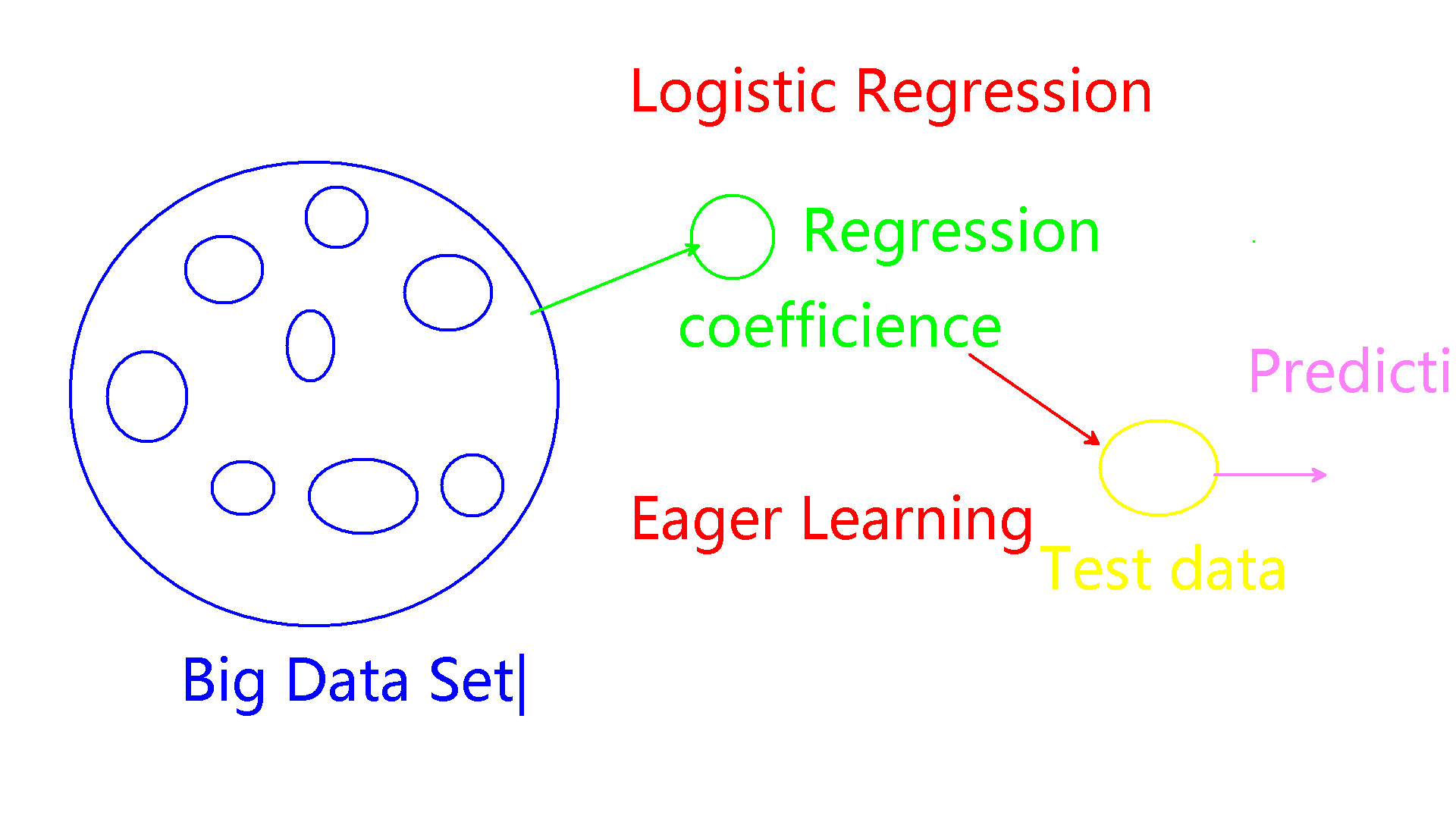
Regression

Logistic Regression逻辑回归，用于二分的数据，比如判断有/没有患病，有/没有风险。

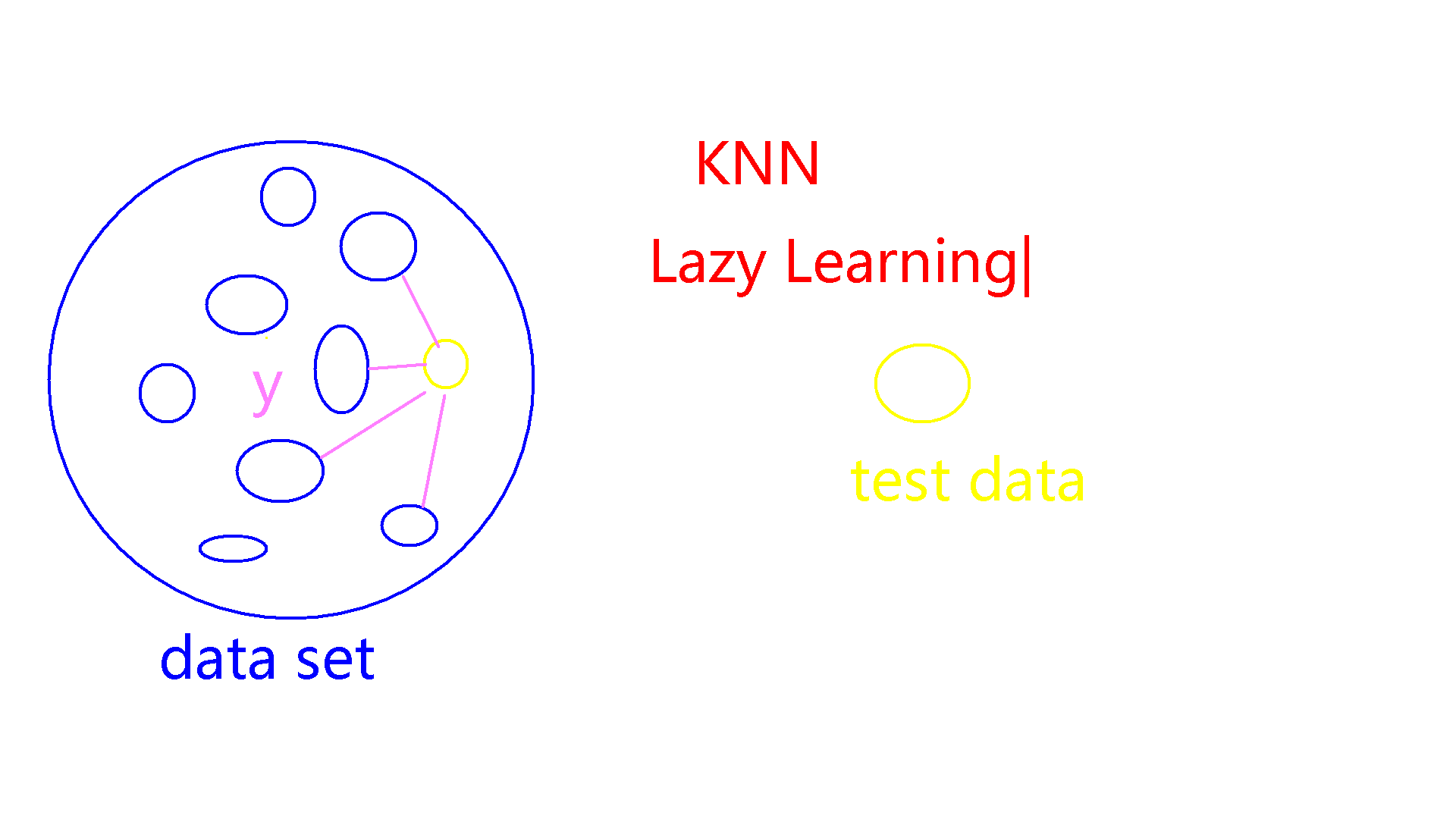
Lazy Learning和Eager Learning

1.KNN算法
每次test_data和数据集中所有数据计算距离，找到最近的作为输出。在测试数据test_data到来之前没有办法得到结果，而且test_data来了之后要花很多时间计算。
因为是直到test_data到来才开始计算，因此这类算法叫做Lazy Learning。不够及时所以不太常用。

2.png


2.Logistic Regression
提前对dataset反复训练，计算好Regression Coefficience回归系数，然后获得test_data之后立刻可以根据Regression Coefficience进行predict获得结果。
因为是拿到训练集数据立刻计算，这类算法叫做Eager Learning。这种方法更常用，更有实际价值。
一般数据中心（云端）从big data set负责计算这样的”经验”，用于在终端中使用。可以快速响应。
4.png

实例

修飞机发动机的老师傅把故障表现存储到数据库中，做成VB程序，让经验不够的徒弟每次遇到问题查询。但这样的方式还不够智能，准确率不够高。最后利用逻辑回归的方式，对每个部件分别评估，得到最终的结果：是否故障（0或1）。
这样的工作会替代重复劳动，是大势所趋。算法、人工智能很重要，懂这些知识才不会失业。

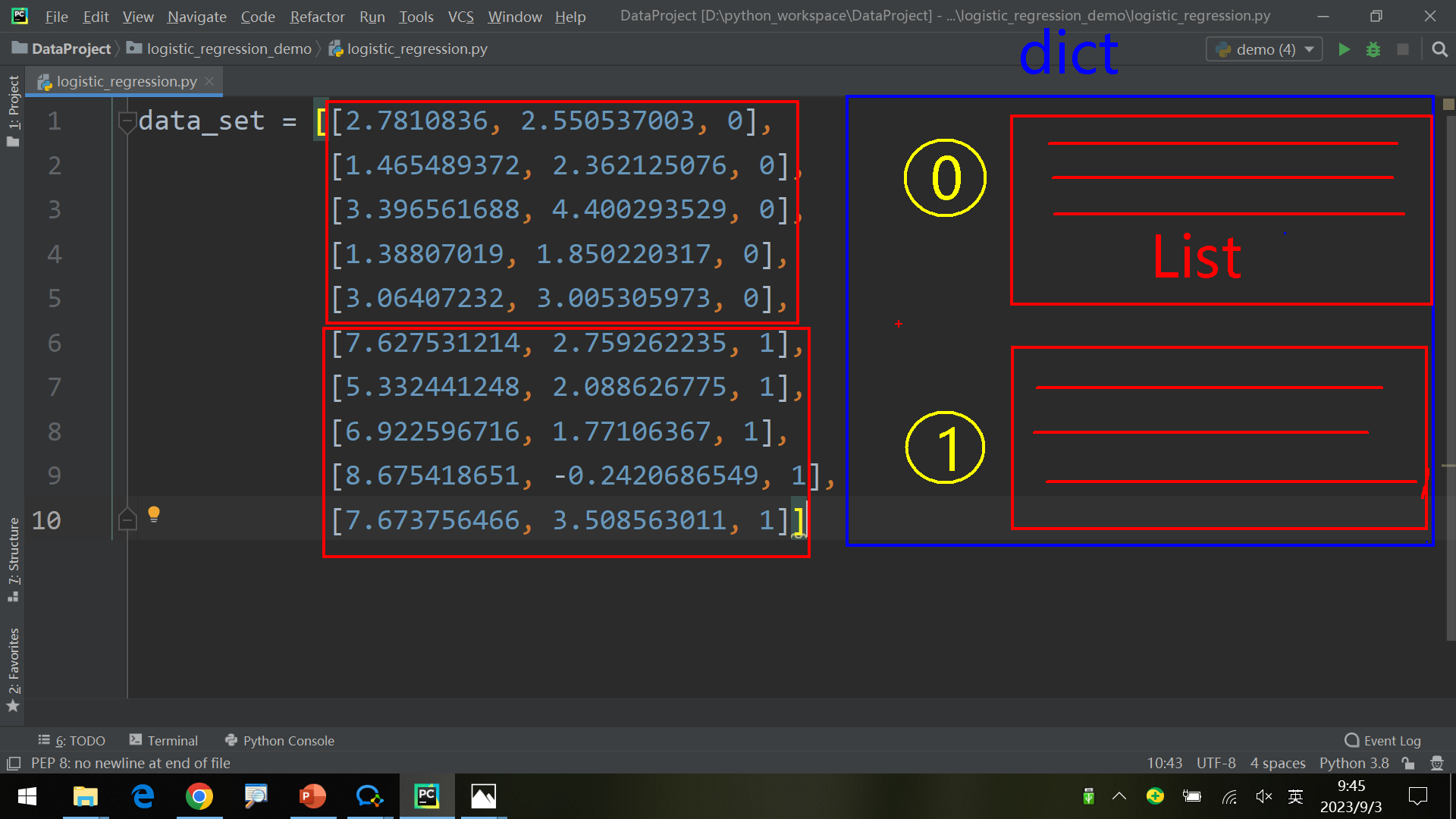
按label分类

如何整理数据，将数据根据label分组?
5.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
data_set = [[2.7810836, 2.550537003, 0],  
            [1.465489372, 2.362125076, 0],  
            [3.396561688, 4.400293529, 0],  
            [1.38807019, 1.850220317, 0],  
            [3.06407232, 3.005305973, 0],  
            [7.627531214, 2.759262235, 1],  
            [5.332441248, 2.088626775, 1],  
            [6.922596716, 1.77106367, 1],  
            [8.675418651, -0.2420686549, 1],  
            [7.673756466, 3.508563011, 1]]  
  
def seperate_by_class(data):  
    seperated_data = dict()  
    for i in range(len(data)):  
        data = data_set[i]  
        label = data[2]  
  
        if label not in seperated_data:  
            seperated_data[label] = []  
        seperated_data[label].append(data)  
    return  seperated_data  
  
if __name__ == "__main__" :  
    print(seperate_by_class(data_set))

输出如下：

{0: [[2.7810836, 2.550537003, 0], [1.465489372, 2.362125076, 0], [3.396561688, 4.400293529, 0], [1.38807019, 1.850220317, 0], [3.06407232, 3.005305973, 0]],
1: [[7.627531214, 2.759262235, 1], [5.332441248, 2.088626775, 1], [6.922596716, 1.77106367, 1], [8.675418651, -0.2420686549, 1], [7.673756466, 3.508563011, 1]]}

获取各列数据、画图

在上述操作的基础上，还可以获取label分组中第i列的数据，如下:

1
2
3
4
5
if __name__ == "__main__" :  
    seperated_data = seperate_by_class(data_set)  
  
    data_set0 = [column for column in zip(*seperated_data[0])]  # 取label=0的数据中的各列数据  
    data_set1 = [column for column in zip(*seperated_data[1])]  # 取label=1的数据中的各列数据  
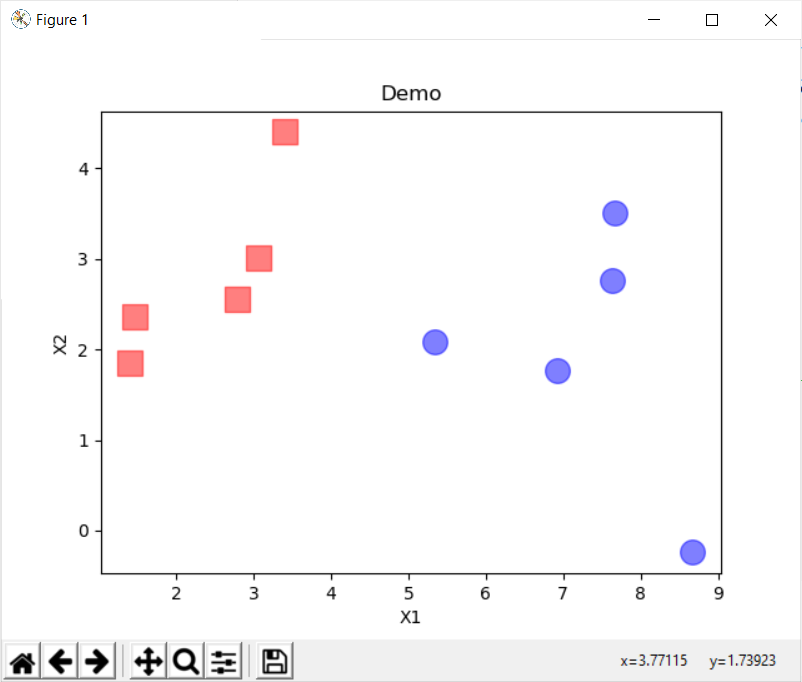
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import  matplotlib.pyplot as plt  
  
data_set = [[2.7810836, 2.550537003, 0],  
            [1.465489372, 2.362125076, 0],  
            [3.396561688, 4.400293529, 0],  
            [1.38807019, 1.850220317, 0],  
            [3.06407232, 3.005305973, 0],  
  
            [7.627531214, 2.759262235, 1],  
            [5.332441248, 2.088626775, 1],  
            [6.922596716, 1.77106367, 1],  
            [8.675418651, -0.2420686549, 1],  
            [7.673756466, 3.508563011, 1]]  
  
def seperate_by_class(data):  
    seperated_data = dict()  
    for i in range(len(data)):  
        data = data_set[i]  
        label = data[2]  
  
        if label not in seperated_data:  
            seperated_data[label] = []  
        seperated_data[label].append(data)  
    return  seperated_data  
  
if __name__ == "__main__" :  
    seperated_data = seperate_by_class(data_set)  
  
    data_set0 = [column for column in zip(*seperated_data[0])]  # 取label=0的数据中的各列数据  
    data_set1 = [column for column in zip(*seperated_data[1])]  # 取label=1的数据中的各列数据  
    print(data_set0)  
    print(data_set1)  
  
    figure = plt.figure()  
    axes = figure.add_subplot()  
    axes.scatter(data_set0[0], data_set0[1], s=200, c='red', marker='s', alpha=.5) # s是大小， c是颜色, marker是形状， alpha透明度
    axes.scatter(data_set1[0], data_set1[1], s=200, c='blue', alpha=.5)  
  
    plt.title('Demo')  
    plt.xlabel('X1')  
    plt.ylabel('X2')  
    plt.show()

输出图像如下：
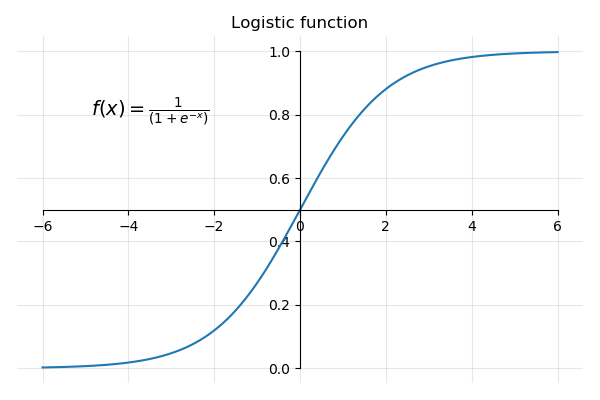
image.png

Logistic Regression逻辑回归模型

image.png

根据x代入函数f(x)中，得到y在第一象限或者第三象限（取决于y大于0.5还是小于0.5）。
如果y>0.5在第一象限，则输出1；否则y<0.5在第三象限，输出0。

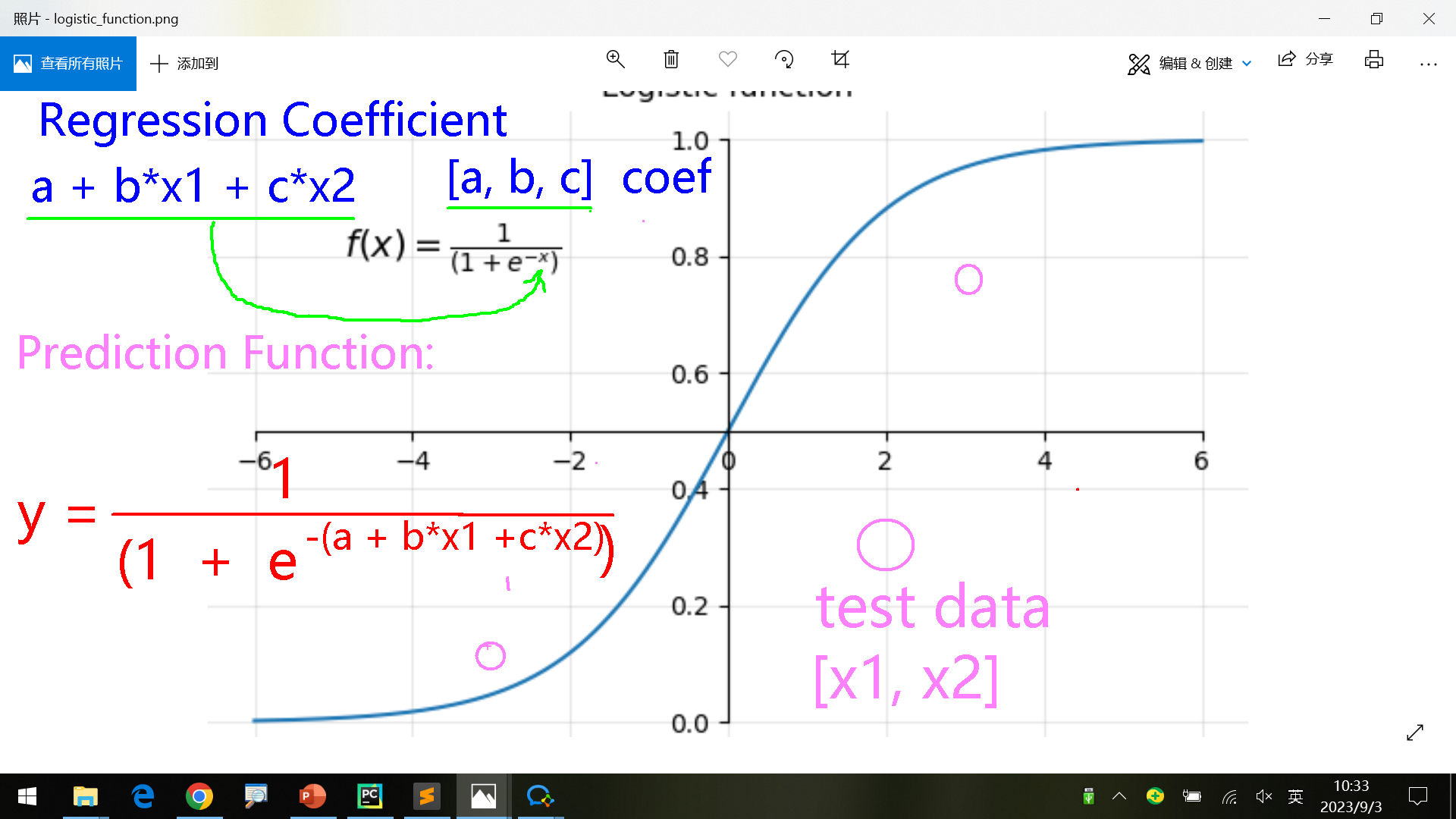
image.png
回归系数取决于结构。
公式:

regression coefficient = a+ b * x1 + c * x2

训练后得到的一组常数[a, b, c]就是coef
当有3个变量时是a+ b * x1 + c * x2 + d * x3, 得到结果是[a, b, c, d]。 以此类推。
学习算法时，一般会列出最终的公式，往往很复杂。可以反过来，把一个n=1,2,3依次代入，方便理解。

prediction function:
将回归系数a+ b * x1 + c * x2代入方程f(x)中的x，得到新的方程y=f’(x1,x2)
获得新的test_data(x1, x2)之后，将它的x1, x2代入f’(x1,x2)得到的y’就是其pred_data。

可能采用不同的梯度算法，但是logistic regression模型原理都相同。一般也不用太深入研究算法原理，更多是利用它进行实际应用

大部分算法都是这个难度，少数比这些更难的算法用的频率也很低。
一般学习算法也没有多难，不要害怕。如果结合生产实践来学习算法会更有意思，更好学习。


代码实现

主要是把前面的数学公式翻译为代码，比较简单。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np  
  
data_set = [[2.7810836, 2.550537003, 0],  
            [1.465489372, 2.362125076, 0],  
            [3.396561688, 4.400293529, 0],  
            [1.38807019, 1.850220317, 0],  
            [3.06407232, 3.005305973, 0],  
  
            [7.627531214, 2.759262235, 1],  
            [5.332441248, 2.088626775, 1],  
            [6.922596716, 1.77106367, 1],  
            [8.675418651, -0.2420686549, 1],  
            [7.673756466, 3.508563011, 1]]  
  
def logistic_regression(x):  
    return  1.0 /( 1+ np.exp(-x))  
  
def predict(test_data, coffiencients):  
    coef_sum = coffiencients[0]  
    for i in range(len(test_data)):  
        coef_sum += coffiencients[i+1] * test_data[i]  
    return 1.0 /( 1+ np.exp(-coef_sum))  
  
if __name__ == "__main__" :  
    coef = [-1.6652041168582101, 2.8997553753773953, -4.293589516352396]  
    test_data = [5.332441248, 2.088626775]  
    y_pred = predict(test_data, coef)  
    print(y_pred) # 小于0.5即为0，大于0.5是1

输出如下：

0.9920756968878671

可以看到，到现在高级阶段就很少用sklearn了，它在行业内做的很好，但是效率等还不够好。实际中往往用它比较少。

这个例子只是展示了如何使用已计算得出的coef来进行计算。实际中还需要计算coef。

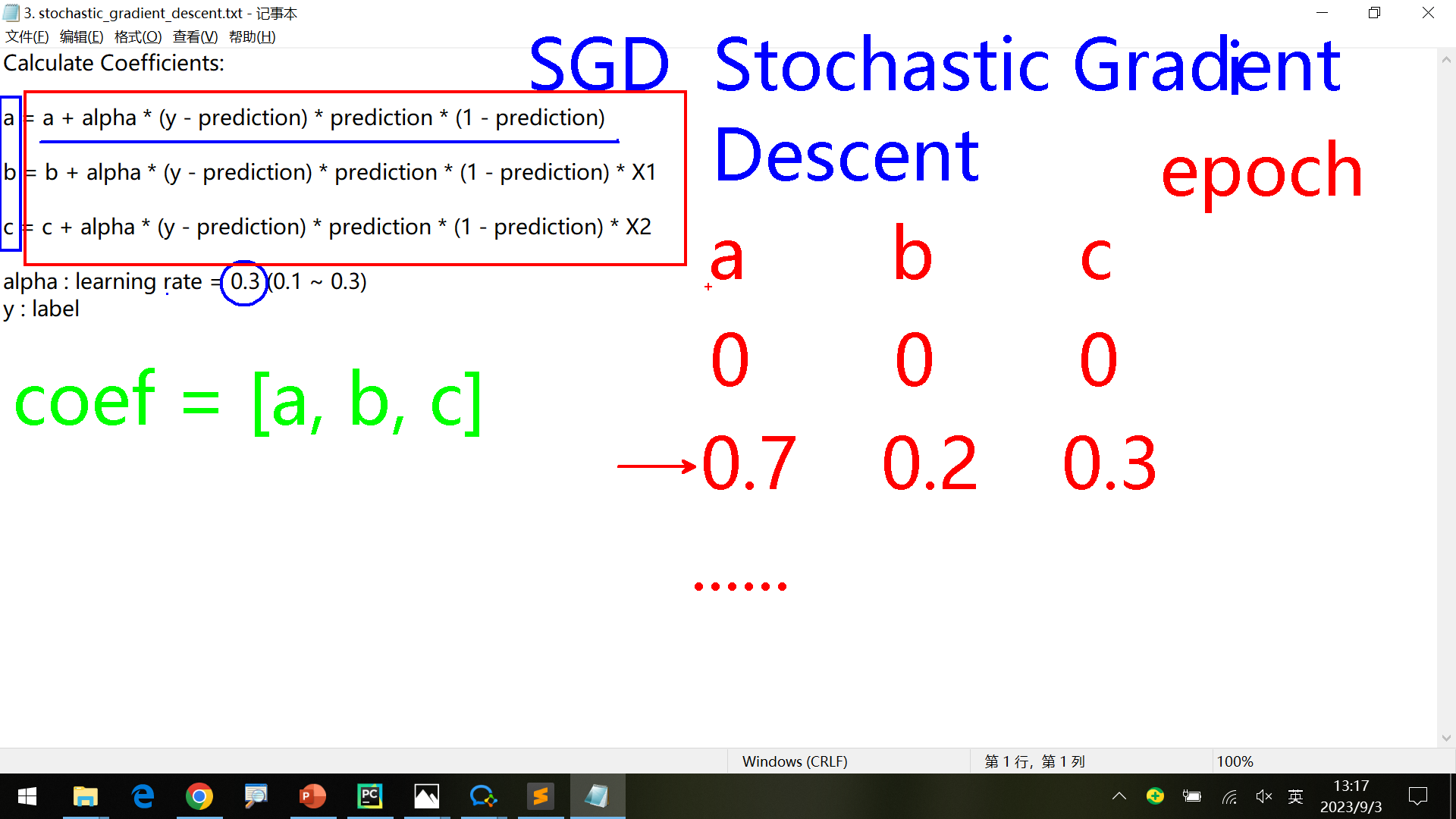
计算coef

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np  
  
data_set = [[2.7810836, 2.550537003, 0],  
            [1.465489372, 2.362125076, 0],  
            [3.396561688, 4.400293529, 0],  
            [1.38807019, 1.850220317, 0],  
            [3.06407232, 3.005305973, 0],  
  
            [7.627531214, 2.759262235, 1],  
            [5.332441248, 2.088626775, 1],  
            [6.922596716, 1.77106367, 1],  
            [8.675418651, -0.2420686549, 1],  
            [7.673756466, 3.508563011, 1]]  
  
def logistic_regression(x):  
    return  1.0 /( 1+ np.exp(-x))  
  
def predict(test_data, coffiencients):  
    coef_sum = coffiencients[0]  
    for i in range(len(test_data) - 1): # 实际训练中可能y不参与，这时候len需要 -1        coef_sum += coffiencients[i+1] * test_data[i]  
    return 1.0 /( 1+ np.exp(-coef_sum))  
  
def estimate_coefficients(train_data_set, l_rate, n_epoch): # 老师从生产上取的代码  
    coef = [0.0 for i in range(len(train_data_set[0]))]  
    for epoch in range(n_epoch):  
        sum_error = 0  
        for row in train_data_set:  
            pred = predict(row, coef)  
            error = row[-1] - pred  
            sum_error += error ** 2  
            coef[0] = coef[0] + l_rate * error * pred * (1.0 - pred)  
            for i in range(len(row) - 1):  
                coef[i + 1] = coef[i + 1] + l_rate * error * pred * (1.0 - pred) * row[i]  
        print('Epoch=%d, Learning Rate=%.3f, Error=%.3f' % (epoch, l_rate, sum_error))  
    return coef  
  
  
if __name__ == "__main__" :  
    l_rate = 0.3  # 系数，0.1-0.3，这里取0.3比较好
    n_epoch = 10000  
    coef = estimate_coefficients(data_set, l_rate, n_epoch)  
    print(coef)

输出如下，省略了一部分：

Epoch=0, Learning Rate=0.300, Error=2.217
Epoch=1, Learning Rate=0.300, Error=1.613
Epoch=2, Learning Rate=0.300, Error=1.113
Epoch=3, Learning Rate=0.300, Error=0.827
Epoch=4, Learning Rate=0.300, Error=0.623
Epoch=5, Learning Rate=0.300, Error=0.494
Epoch=6, Learning Rate=0.300, Error=0.412
Epoch=7, Learning Rate=0.300, Error=0.354
Epoch=8, Learning Rate=0.300, Error=0.310
Epoch=9, Learning Rate=0.300, Error=0.276
……
Epoch=9998, Learning Rate=0.300, Error=0.000
Epoch=9999, Learning Rate=0.300, Error=0.000
[-1.6652041168582128, 2.8997553753773957, -4.293589516352396]

计算coef使用了随机梯度下降（stochastic gradient descent，SGD）算法，另外还有随机梯度上升算法。

image.png

a’ = a + …
b’ = b + …
c’ = c + …

为了计算[a,b,c]开始默认a=0, b=0, c=0。首先根据第一组数据计算得到新的(a’, b’, c’)，然后第二组时，使用上组数据得到的(a’, b’, c’)作为系数，根据第二组数据计算得到新的系数(a’‘, b’’, c’‘)，依次类推。

同样的数据，需要多次学习才可以不断提示正确率。因此需要多轮学习（n_epoch很大），使其不断收敛。
类似导弹发射，在发送出去后可能多次改变方向进行纠正。学习控制论。

数据量很大时，同样计算一万、十万等轮数会非常耗时。生产上，计算中心的云cloud负责计算coef， 用户端只使用这些。

应用

下面是在之前的代码基础上，最简单的样例代码。这里使用了第三方库，还要优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import pandas as pd
from logistic_regression_demo.logistic_regression import estimate_coefficients
from sklearn.preprocessing import MinMaxScaler
from logistic_regression_demo.logistic_regression import predict

# Step 1
data_set = pd.read_csv('pima-indians-diabetes.csv')
mms = MinMaxScaler()
data_set_new = mms.fit_transform(data_set)
coef = estimate_coefficients(data_set_new, 0.3, 10000)
print(coef)

# Step 2

# coef = [-6.600158139331833, -3.3750503590578553, 2.5060952000369974, 5.133947009439194, -4.702571656346261, 1.0079919534754893, 1.4104913560133263, 9.44513302437111, -0.6005167137398385, -0.2821473672340299]
test_data = [2,1,85,66,29,0,26.6,0.351,31,0]
y_pred = predict(test_data, coef)
print(y_pred)

首先像实际开发一样，自己实现读取数据的功能。

读取数据

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from  csv import  reader

def load_data(path):  
    data_set = []  
    with open(path, mode='r', encoding='UTF-8-sig') as file:  
        lines = reader(file)  
        for line in lines :  
            if not line:  
                continue  
            data_set.append(line)  
    return  data_set  
  
data_set = load_data("../pima-indians-diabetes.csv")  
print(data_set)

很多第三方库更新不稳定，可能后面的更新会有很大修改，甚至废弃。这样依赖于第三方库的后期代码维护会困难。

解决方案：

  1. 首选自己实现这样的功能。一是避免后期的问题，二是可以完全自定义，比较灵活。
  2. 其次如果没有能力，也可以写个wrapper将其包装，代码中全部调用这个wrapper而不是原生第三方接口。后面如果第三方api发生变更或者需要自定义修改，只需要改这一个地方。

但是还有个问题，读取的数字是字符串格式，比如是字符串’12.1’而不是数字12.1。下面进行格式转换。

转换字符串到数字

下面的代码将数据集（输入全部是数据，即不包含表头）转换为数字格式：

1
2
3
4
5
def convert_to_float(data_set):  
    for data in data_set: # 一行/组数据  
        for i in range(len(data) - 1) : #每组遍历最后一列（label）除外的每个数据  
            data[i] = float(data[i].strip())  
    return  data_set

注意这个函数的输入只接受数据，不能将表头等不是数字的数据传入。

转换后的数据（省略部分）：

[[1.0, 6.0, 148.0, 72.0, 35.0, 0.0, 33.6, 0.627, 50.0, ‘1’],
[2.0, 1.0, 85.0, 66.0, 29.0, 0.0, 26.6, 0.351, 31.0, ‘0’],
[3.0, 8.0, 183.0, 64.0, 0.0, 0.0, 23.3, 0.672, 32.0, ‘1’],
…
[1.0, 0.10201280878316561, 0.2564102564102564, ‘1’]]

下面还需要自己实现对数据的预处理，以代替原来的MinMaxScaler。

预处理

sklearn中的代码写的不错，虽然没有考虑到太多性能、大数据量下的情况等，但是命名规范、算法实现、文档等都可以参考、学习。

查看sklearn的MinMaxScaler()函数注释：

The transformation is given by:

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min

where min, max = feature_range.

其中axis表示行或者列，axis=0表示列，axis=1表示行。
缩放分2步：1.计算每列最小最大值、2.计算X_std进行缩放。

第一部分：计算每列最小最大值

1
2
3
4
5
6
7
8
9
# preprocessing: part I
def find_min_max(data_set):  
    min_max_list = []  
    for i in range( len(data_set[0] )): # i是列数  
        col = [data[i] for  data in data_set] #取第i列  
        min_value = min(col)  
        max_value = max(col)  
        min_max_list.append(min_value, max_value)  
    return  min_max_list

第二部分：计算X_std进行缩放

1
2
3
4
5
6
# preprocessing: part II  
def min_max_scaler(data_set, min_max):  
    for data in data_set:  
        for i in range(len(data) - 1): #遍历每组的各个字段  
            data[i] = (data[i] - min_max[i][0]) / (min_max[i][1] - min_max[i][0])  
    return data_set

转换后的数据（省略部分）：

[[0.0, 0.4, 0.751269035532995, 0.6545454545454545, 0.5833333333333334, 0.0, 0.676056338028169, 0.24016468435498628, 0.7435897435897436, ‘1’],
[0.010101010101010102, 0.06666666666666667, 0.43147208121827413, 0.6, 0.48333333333333334, 0.0, 0.5352112676056338, 0.11390667886550777, 0.2564102564102564, ‘0’],
[0.020202020202020204, 0.5333333333333333, 0.9289340101522843, 0.5818181818181818, 0.0, 0.0, 0.46881287726358145, 0.26075022872827086, 0.28205128205128205, ‘1’],
…
[1.0, 0.06666666666666667, 0.6192893401015228, 0.8181818181818182, 0.85, 0.26004728132387706, 1.0, 0.10201280878316561, 0.2564102564102564, ‘1’]]

实际应用分为2步，第一步计算coef，第二步使用它进行预测。

应用：计算coef

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# step 1 计算coef  
  
# data_set = data_set = pd.read_csv('pima-indians-diabetes.csv') # 使用第三方库  
data_set = convert_to_float(load_data("../pima-indians-diabetes.csv")[1:]) # 遍历第一行（title）除外的每组数据  
# print(data_set)  
  
# 预处理，不进行预处理会出错  
# mms = MinMaxScaler() # 使用第三方库  
# data_set_new = mms.fit_transform(data_set)  
  
min_max_list = find_min_max(data_set)  
data_set_new = min_max_scaler(data_set, min_max_list)  
# print(data_set_new)  
  
coef = estimate_coefficients(data_set_new, 0.3, 1000)  
# print(coef)

应用：预测

1
2
3
4
5
6
# Step 2 predict预测  
  
# coef = [-6.6001596766267765, -3.3750522046460594, 2.506096706072231, 5.133948235459311, -4.702575087818696, 1.007991983984168, 1.4104935617389902, 9.44513792712282, -0.6005169020203235, -0.28214794688926603]  
test_data = [2,1,85,66,29,0,26.6,0.351,31,0] # 随便找的一组数据作为测试数据  
y_pred = predict(test_data, coef)  
print(y_pred)

完整代码

logistic_regression2.calc_coef文件： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  
def predict(test_data, coffiencients):  
    coef_sum = coffiencients[0]  
    for i in range(len(test_data) - 1): # 实际训练中可能y不参与，这时候len需要 -1        coef_sum += coffiencients[i+1] * test_data[i]  
    return 1.0 /( 1+ np.exp(-coef_sum))  
  
def estimate_coefficients(train_data_set, l_rate, n_epoch): # 老师从生产上取的代码  
    coef = [0.0 for i in range(len(train_data_set[0]))]  
    for epoch in range(n_epoch):  
        sum_error = 0  
        for row in train_data_set:  
            pred = predict(row, coef)  
            error = row[-1] - pred  
            sum_error += error ** 2  
            coef[0] = coef[0] + l_rate * error * pred * (1.0 - pred)  
            for i in range(len(row) - 1):  
                coef[i + 1] = coef[i + 1] + l_rate * error * pred * (1.0 - pred) * row[i]  
        print('Epoch=%d, Learning Rate=%.3f, Error=%.3f' % (epoch, l_rate, sum_error))  
    return coef

主要文件： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
from logistic_regression2.calc_coef import estimate_coefficients  
from logistic_regression2.calc_coef import predict  
from  csv import  reader  
  
  
def load_data(path):  
    data_set = []  
    with open(path, mode='r', encoding='UTF-8-sig') as file:  
        lines = reader(file)  
        for line in lines :  
            if not line:  
                continue  
            data_set.append(line)  
    return  data_set  
  
def convert_to_float(data_set):  
    for data in data_set: # 一行/组数据  
        for i in range(len(data) ) : #每组遍历最后一列（label）除外的每个数据  
            data[i] = float(data[i].strip())  
    return  data_set  
  
# preprocessing: part I  
def find_min_max(data_set):  
    min_max_list = []  
    for i in range( len(data_set[0] )): # i是列数  
        col = [data[i] for  data in data_set] #取第i列  
        min_value = min(col)  
        max_value = max(col)  
        min_max_list.append((min_value, max_value))  
    return  min_max_list  
  
# preprocessing: part II  
def min_max_scaler(data_set, min_max):  
    for data in data_set:  
        for i in range(len(data) ): #遍历每组的各个字段  
            data[i] = (data[i] - min_max[i][0]) / (min_max[i][1] - min_max[i][0])  
    return data_set  
  
# step 1 计算coef  
  
# data_set = data_set = pd.read_csv('pima-indians-diabetes.csv') # 使用第三方库  
data_set = convert_to_float(load_data("../pima-indians-diabetes.csv")[1:]) # 遍历第一行（title）除外的每组数据  
# print(data_set)  
  
# 预处理，不进行预处理会出错  
# mms = MinMaxScaler() # 使用第三方库  
# data_set_new = mms.fit_transform(data_set)  
  
min_max_list = find_min_max(data_set)  
data_set_new = min_max_scaler(data_set, min_max_list)  
# print(data_set_new)  
  
coef = estimate_coefficients(data_set_new, 0.3, 1000)  
# print(coef)  
  
# Step 2 predict预测  
  
# coef = [-6.6001596766267765, -3.3750522046460594, 2.506096706072231, 5.133948235459311, -4.702575087818696, 1.007991983984168, 1.4104935617389902, 9.44513792712282, -0.6005169020203235, -0.28214794688926603]  
test_data = [2,1,85,66,29,0,26.6,0.351,31,0] # 随便找的一组数据作为测试数据  
y_pred = predict(test_data, coef)  
print(y_pred)

输出如下：

Epoch=0, Learning Rate=0.300, Error=22.999
Epoch=1, Learning Rate=0.300, Error=22.595
Epoch=2, Learning Rate=0.300, Error=21.533
……
Epoch=997, Learning Rate=0.300, Error=16.441
Epoch=998, Learning Rate=0.300, Error=16.440
Epoch=999, Learning Rate=0.300, Error=16.440
1.0

无监督学习

无监督学习中，数据是没有label列的，需要经过机器学习划分分组、加上label。
例如KMean算法，根据数据，将相似的客户分为不同的组。

customer.txt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
customer1,1.69,0.14,-0.636,0.069,-0.337
customer2,1.69,-0.322,0.852,0.844,-0.554
customer3,1.682,-0.488,-0.211,0.159,-0.1095
customer4,1.534,-0.785,0.002,0.273,-1.149
customer5,0.890,-0.427,-0.636,-0.604,-0.391
customer6,-0.233,-0.691,-0.636,-0.604,-0.391
customer7,-0.497,1.996,-0.707,-0.662,-1.311
customer8,-0.869,-0.268,-0.281,-0.262,3.396
customer9,-1.075,0.025,-0.423,-0.521,0.150
customer10,1.907,-0.884,2.979,2.130,0.366
customer11,0.478,-0.565,0.825,-0.068,-0.662
customer12,0.469,-0.939,0.073,-0.301,3.288
customer13,0.369,0.747,-0.636,-0.626,-0.283
customer14,0.453,1.517,0.073,-0.301,3.288
customer15,0.369,-.747,-0.636,-0.626,-0.283
customer16,0.312,-0.896,0.498,0.954,-0.500
customer17,-0.026,-0.681,0.073,0.325,0.366
customer18,-0.051,2.723,-0.636,-0.749,0.799
customer19,-0.092,2.879,-0.707,-0.734,-0.662
customer20,-0.150,-0.521,1.278,1.392,1.124

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from sklearn.cluster import  KMeans  
  
def load_data(path):  
    file = open(path, 'r')  
    lines = file.readlines()  
    data_set = []  
    customer_names = []  
    for line in lines:  
        items = line.strip().split(',')  
        customer_names.append(items[0])  
        data_set.append([float(items[i]) for i in range(1, len(items))])  
    return  data_set, customer_names  
  
if __name__ == "__main__":  
    data_set, customer_names = load_data('./customer.txt')  
    # print(data_set)  
    # print(customer_names)    kmeans = KMeans(n_clusters=3)  
    labels = kmeans.fit_predict(data_set)  
    print(labels)  
    customer_cluster = [[], [], []]  
    for i in range(len(customer_names)):  
        customer_cluster[labels[i]].append(customer_names[i])  
    for i in range(len(customer_cluster)):  
        print(customer_cluster[i])

输出如下：

[1 1 1 1 1 1 2 0 2 1 1 0 2 0 1 1 1 2 2 1]
[‘customer8’, ‘customer12’, ‘customer14’]
[‘customer1’, ‘customer2’, ‘customer3’, ‘customer4’, ‘customer5’, ‘customer6’, ‘customer10’, ‘customer11’, ‘customer15’, ‘customer16’, ‘customer17’, ‘customer20’]
[‘customer7’, ‘customer9’, ‘customer13’, ‘customer18’, ‘customer19’]

工作相关

未来这种会是1主流。

需要懂编程，同时也懂算法，结合在一起才可以，大学的数学知识够用。
实例：招数学系的第一次用github把仓库锁住，所有人无法提交；第一次写java变量名写x1, x2, x3……x20

这种工作不是培训几个月就可以上手的，一定是前期做过开发、有一定经验，后面慢慢学习、转变等。