复习
上一节的内容被称作traingin model, 主要是根据big data set计算获得coefficient的过程;
可以不懂公式的具体原理,但是要知道每个参数的含义、如何使用算法、用代码实现算法 ;
利用SGD随机梯度下降算法计算coef;
这一节课主要讲贝叶斯公式Bayes’ theorem
如何用已知预测未知
Prediction Model训练模型Training Model 和预测模型Prediction Model ,这一节也会使用贝叶斯算法实现这两个模型
Bayes’ theorem and Prediction Model
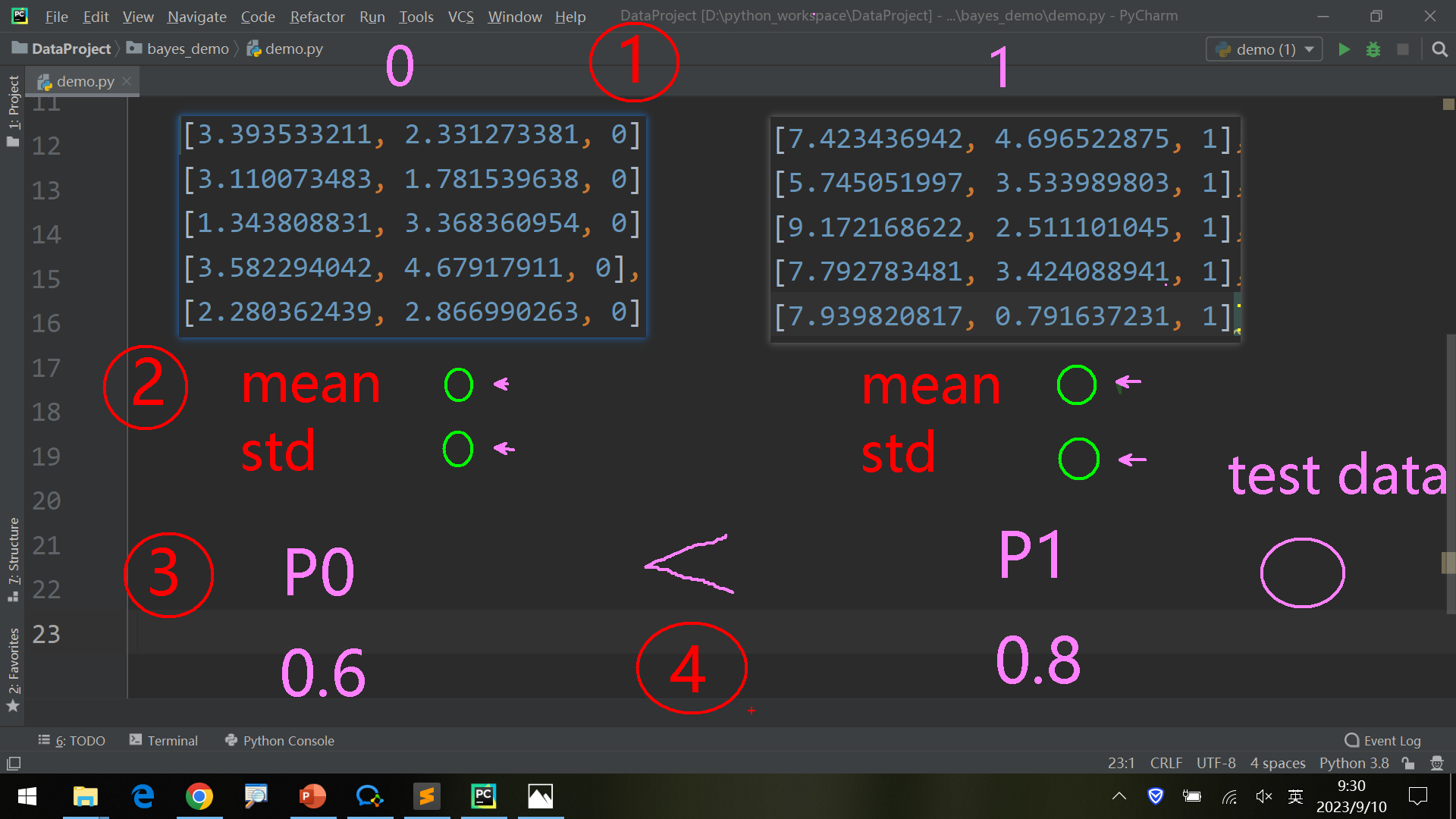
Prediction Model流程如下,主要分为训练和预测:
数据根据label(y=0, y=1, ……)分组为G1, G2 …. Gn;
对每组的每一列[X1, X2, …. Xn],计算各个均值mean和标准差std;
根据test_data,计算各组的概率P0, P1……
输出可能性最大的组对应的label。
1.分组 这里使用上一周的函数seperate_by_class
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 data_set = [[3.393533211 , 2.331273381 , 0 ], [3.110073483 , 1.781539638 , 0 ], [1.343808831 , 3.368360954 , 0 ], [3.582294042 , 4.67917911 , 0 ], [2.280362439 , 2.866990263 , 0 ], [7.423436942 , 4.696522875 , 1 ], [5.745051997 , 3.533989803 , 1 ], [9.172168622 , 2.511101045 , 1 ], [7.792783481 , 3.424088941 , 1 ], [7.939820817 , 0.791637231 , 1 ]] def seperate_by_class (data ): seperated_data = dict () for i in range (len (data)): data = data_set[i] label = data[2 ] if label not in seperated_data: seperated_data[label] = [] seperated_data[label].append(data) return seperated_data if __name__ == "__main__" : print (seperate_by_class(data_set))
输出如下:
{0: [[3.393533211, 2.331273381, 0], [3.110073483, 1.781539638, 0], [1.343808831, 3.368360954, 0], [3.582294042, 4.67917911, 0], [2.280362439, 2.866990263, 0]],
2.计算各列mean和std
尽量看英文书籍、因为同一个英文数学术语可能被翻译为不同的术语。例如Confusion matrix:混淆矩阵、误差矩阵等。
写计算均值和方差的函数,然后对各列计算均值、方差:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def mean (numbers ): return sum (numbers)/len (numbers) def standard_deviation (numbers ): avg = mean(numbers) variance = sum ( [(a - avg) ** 2 for a in numbers ]) / len (numbers) return sqrt(variance) def sumarize (numbers ): return [(mean(a), standard_deviation(a), len (a)) for a in zip (*numbers)]
执行print(sumarize(data_set))测试,输出如下:
[(5.178333386499999, 2.624612513030006, 10), (2.9984683241, 1.1560240509233746, 10), (0.5, 0.5, 10)]
最后进行分组,对每组调用sumarize计算mean, std:
1 2 3 4 5 6 7 8 9 10 def summarize_by_class (data_set ): seperated = seperate_by_class(data_set) summaries = {} for label, data in seperated.items(): summaries[label] = sumarize(data) return summaries
输出如下:
{0: [(2.7420144012, 0.8287479077141687, 5), (3.0054686692, 0.9904256942385166, 5), (0.0, 0.0, 5)], 1: [(7.6146523718, 1.1041096849046812, 5), (2.9914679790000003, 1.3006698840042743, 5), (1.0, 0.0, 5)]}
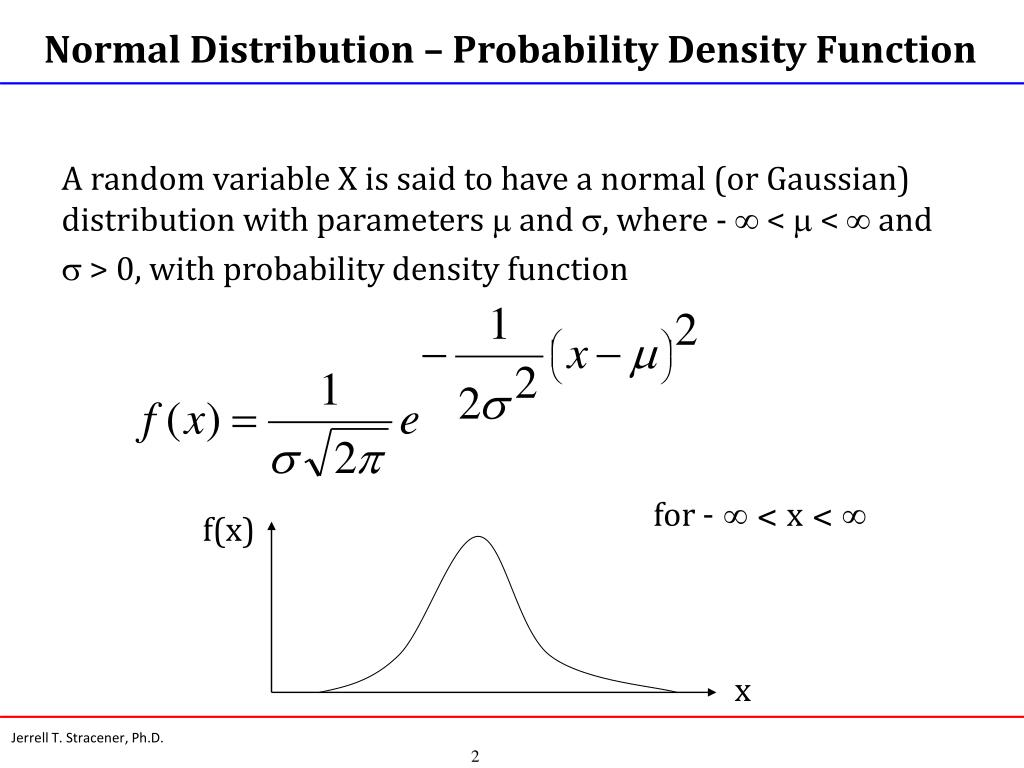
3.计算各组概率P 对下面的公式进行翻译,写为python代码
1 2 3 4 def calculate_probability (x, mean, std ): power = -(x - mean)**2 / (2 * (std**2 )) return (math.e ** power) / (std * math.sqrt(2 * math.pi))
测试
1 2 3 4 if __name__ == "__main__" : print (calculate_probability(1.0 , 1.0 , 1.0 )) print (calculate_probability(0.0 , 1.0 , 1.0 )) print (calculate_probability(2.0 , 1.0 , 1.0 ))
0.3989422804014327
由于是正态分布,x=0和x=2的情况下概率基本相等,符合预期。
前面的公式中,只有1个变量x,但实际中往往有多个,这就需要在实际应用中进行转换。
4.朴素贝叶斯 定义“label值为y(y=0,1,……)”事件A,定义”数据X(x1, x2, …)”为事件B,2者为独立事件。因此,预测在数据X=(x1, x2, …)的情况下label值为y的概率的问题,转换为计算事件B发生的情况下事件A发生的概率,也即**P(A|B)**。
先验概率(A发生的条件下,B发生的概率)——公式1:
P(B|A) = P(A and B) / P(A) (1)
后验概率(B发生的条件下,A发生的概率,用于预测未来)——公式2:
P(A|B) = P(A and B) / P(B) (2)
将1中的P(A and B) = P(B|A) * P(A) 代入公式2,得到:
P(A|B) = P(A and B) / P(B) = (P(B|A) * P(A) ) / P(B)
由于P(B)计算比较麻烦,而实际中只需要为了对比(不同label发生的)概率,得到最高的那个,不需要真正计算,因此可以省去除以P(B),这样会更方便 ,因为不影响比较的结果。Naïve Bayes 。
实际中使用的(朴素)贝叶斯公式如下:
P(class|X) = P(X|class) * P(class)
以X=[X1, X2]为例,公式如下:
从集合的角度来看,A发生同时B发生的概率取决于集合A、B的相交部分大小。因此提升准确率的方法有2个方向:1.提升训练集的数据量(让A、B的相交部分,即训练和测试y相似部分尽量扩大 );2.提升算法准确率。
朴素贝叶斯公式的实现:
1 2 3 4 5 6 7 8 9 def calculate_class_probabilities (summaries, test_data ): total_rows = sum ([summaries[label][0 ][2 ] for label in summaries]) probabilities = dict () for class_value, class_summaries in summaries.items(): probabilities[class_value] = summaries[class_value][0 ][2 ] / total_rows for i in range (len (class_summaries)): mean, std, count = class_summaries[i] probabilities[class_value] *= calculate_probability(test_data[i], mean, std) return probabilities
代码解释: 首先total_rows是取总行数,即各label的行数相加。以下面的summaries为例,label只有2个:0和1,total_rows=5+5=10。
{0: [(2.7420144012, 0.8287479077141687, 5), (3.0054686692, 0.9904256942385166, 5)], 1: [(7.6146523718, 1.1041096849046812, 5), (2.9914679790000003, 1.3006698840042743, 5)]}
for class_value, class_summaries in summaries.items()这一句遍历summaries,取每个(label, [对应label各列的(mean, std, rows)元组])。其中class_value也就是label。
probabilities[class_value]是计算P(class=label)的概率,也就是label对应行数/总行数。 在内部的循环for i in range(len(class_summaries)):中,每次取出label一列的mean, std和count,并且使用calculate_probability根据正态分布计算概率,也即P(X1|class=label),最后和probabilities[class_value]相乘,设为新的probabilities[class_value]。
以之前的数据为例,probabilities字典的变化如下:
class_value=0, class_summaries= [(2.7420144012, 0.8287479077141687, 5), (3.0054686692, 0.9904256942385166, 5)]
class_value=1, class_summaries= [(7.6146523718, 1.1041096849046812, 5), (2.9914679790000003, 1.3006698840042743, 5)]
参考:naive_bayes算法训练Iris数据 从读取数据到处理数据、计算概率、比较并输出label
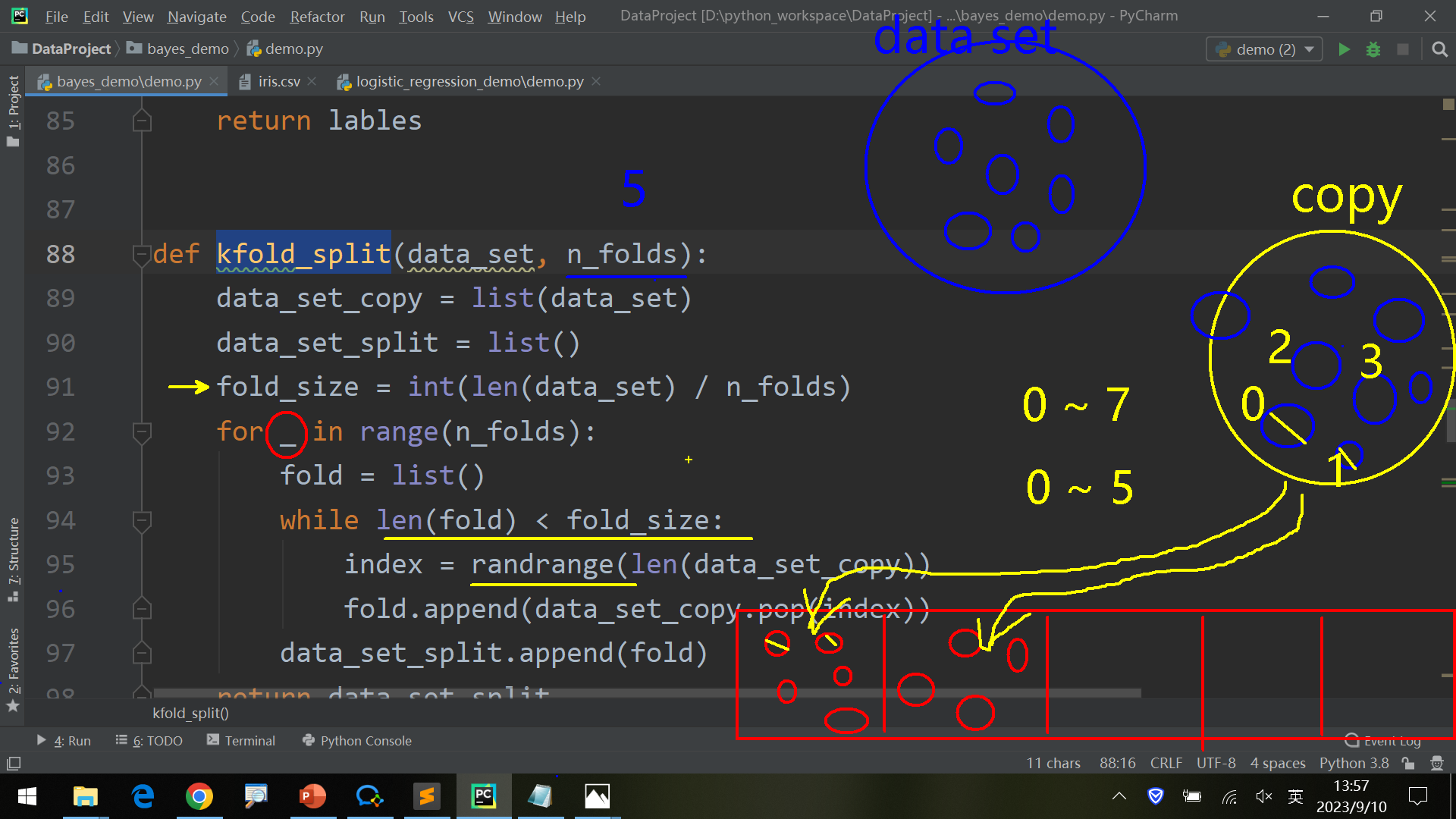
计算组数、数据随机抽样填充每一组
遍历,每次从列表中抽出第i组作为test_data,其余作为train_data进行训练和预测。
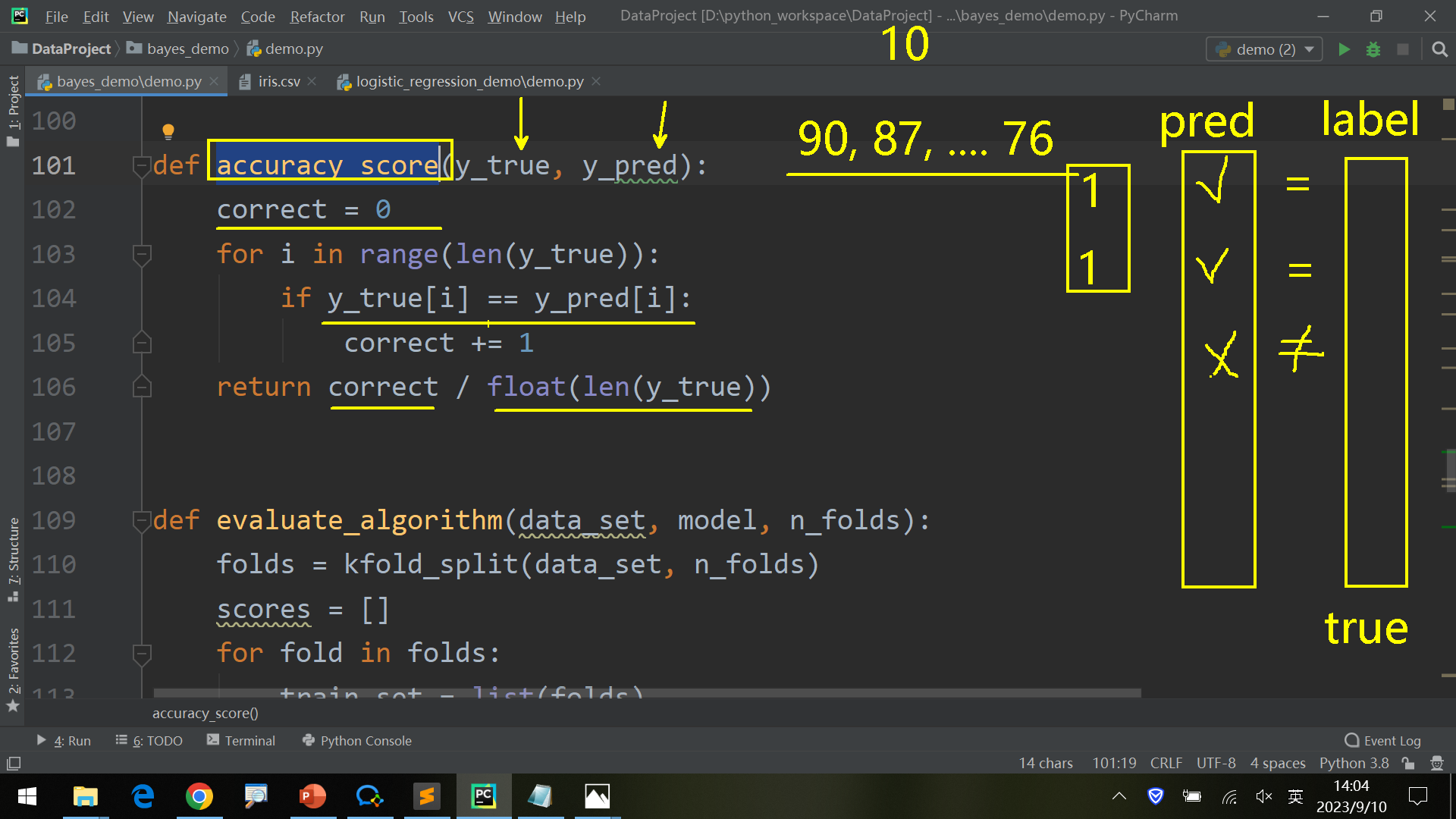
比较正确结果,计算准确率
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 from math import sqrtfrom math import pifrom math import expfrom csv import readerfrom random import randrangedef separate_by_class (data_set ): separated_data_set = dict () for i in range (len (data_set)): data = data_set[i] label = data[-1 ] if label not in separated_data_set: separated_data_set[label] = list () separated_data_set[label].append(data) return separated_data_set def mean (numbers ): return sum (numbers) / len (numbers) def standard_deviation (numbers ): avg = mean(numbers) variance = sum ([(n - avg) ** 2 for n in numbers]) / len (numbers) return sqrt(variance) def summarize (data_set ): summaries = [(mean(column), standard_deviation(column), len (column)) for column in zip (*data_set)] del (summaries[-1 ]) return summaries def summarize_by_class (data_set ): separated_data_set = separate_by_class(data_set) summaries = dict () for label, data in separated_data_set.items(): summaries[label] = summarize(data) return summaries def calculate_probability (x, mean, std ): exponent = exp(-(x - mean) ** 2 / (2 * std **2 )) return (1 / (std * sqrt(2 * pi))) * exponent def calculate_class_probabilities (summaries, test_data ): total_rows = sum ([summaries[label][0 ][2 ] for label in summaries]) probabilities = dict () for class_value, class_summaries in summaries.items(): probabilities[class_value] = summaries[class_value][0 ][2 ] / total_rows for i in range (len (class_summaries)): mean, std, count = class_summaries[i] probabilities[class_value] *= calculate_probability(test_data[i], mean, std) return probabilities def load_data (path ): data_set = [] with open (path, 'r' ) as file: lines = reader(file) for line in lines: if not line: continue data_set.append(line) return data_set def convert_to_float (data_set ): for data in data_set: for i in range (len (data) - 1 ): data[i] = float (data[i].strip()) def label_encoder (data_set ): label_column = len (data_set[0 ]) - 1 class_values = [data[label_column] for data in data_set] class_set = set (class_values) lables = dict () for i, value in enumerate (class_set): lables[value] = i for data in data_set: data[label_column] = lables[data[label_column]] return lables def kfold_split (data_set, n_folds ): data_set_copy = list (data_set) data_set_split = list () fold_size = int (len (data_set) / n_folds) for _ in range (n_folds): fold = list () while len (fold) < fold_size: index = randrange(len (data_set_copy)) fold.append(data_set_copy.pop(index)) data_set_split.append(fold) return data_set_split def accuracy_score (y_true, y_pred ): correct = 0 for i in range (len (y_true)): if y_true[i] == y_pred[i]: correct += 1 return correct / float (len (y_true)) def evaluate_algorithm (data_set, model, n_folds ): folds = kfold_split(data_set, n_folds) scores = [] for fold in folds: train_set = list (folds) train_set.remove(fold) train_set = sum (train_set, []) test_set = [] for row in fold: row_copy = list (row) row_copy[-1 ] = None test_set.append(row_copy) predicted = model(train_set, test_set) actual = [row[-1 ] for row in fold] score = accuracy_score(actual, predicted) scores.append(score) return scores def predict (summaries, test_data ): probabilities = calculate_class_probabilities(summaries, test_data) best_label, best_prob = None , -1 for class_value, probability in probabilities.items(): if best_label is None or probability > best_prob: best_prob = probability best_label = class_value return best_label def naive_bayes (train_set, test_set ): summaries = summarize_by_class(train_set) predictions = list () for test_data in test_set: y_pred = predict(summaries, test_data) predictions.append(y_pred) return predictions if __name__ == '__main__' : data_set = load_data('iris.csv' ) convert_to_float(data_set) print (data_set) label_encoder(data_set) print (data_set) model = summarize_by_class(data_set) test_data = [5.7 , 2.9 , 4.2 , 1.3 ] label = predict(model, test_data) print ('Data=%s, Predicted: %s' % (test_data, label))
这里predict函数是根据calculate_class_probabilities函数返回的各个 (label, possibility) 对找到概率最高的一个label,将其作为y_pred输出。
预测模型和naive_bayes函数都是先后调用summarize_by_class对训练数据分组后再调用predict(train_data, test_data)输出对于test_data概率最高的label。
evaluate_algorithm步骤更多一点:
kfold_split将train_data分组为folds 遍历folds
当前组作为test_data_set,其余组为train_data_set
对test_data_set预测predict
accuracy_score比对预测结果和实际结果,得到正确率
输出正确率集合scores
实现StratifiedKFold 在前面老师的代码中使用测试数据、打印内容查看具体执行步骤:
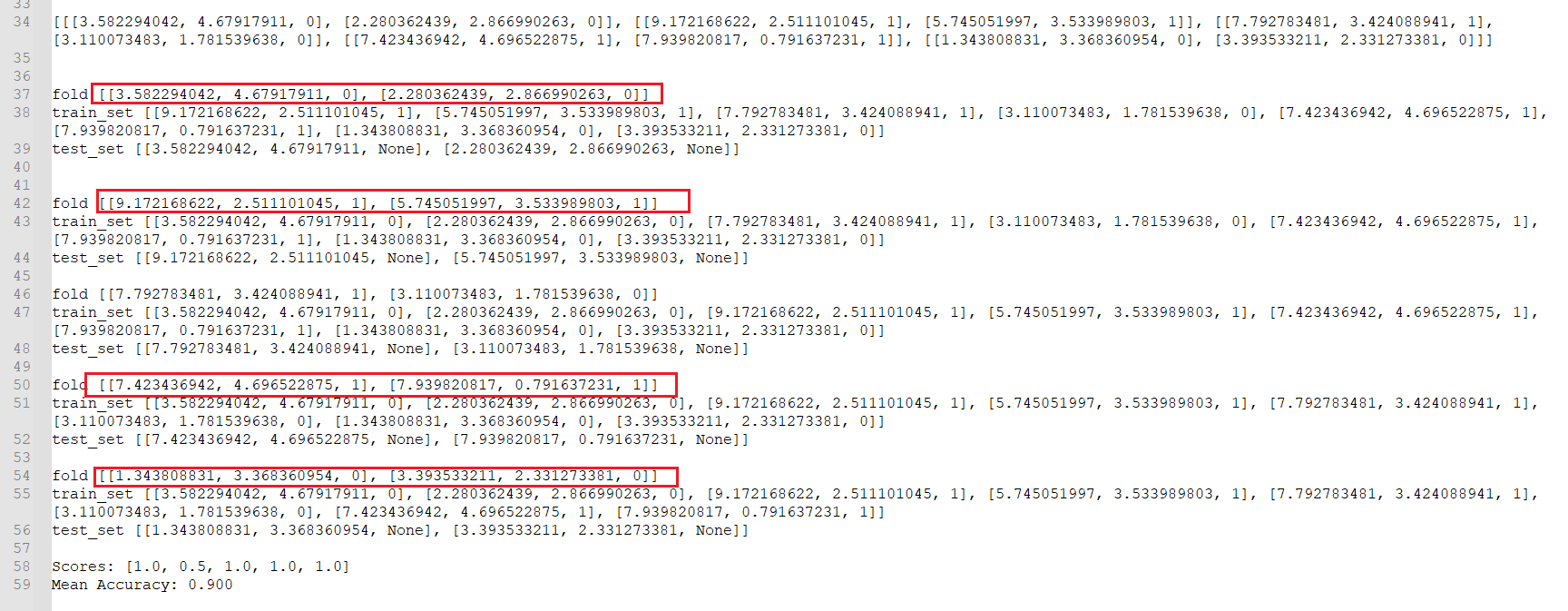
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 from math import sqrt from math import pi from math import exp from csv import reader from random import randrange data_set_demo = [[3.393533211 , 2.331273381 , 0 ], [3.110073483 , 1.781539638 , 0 ], [1.343808831 , 3.368360954 , 0 ], [3.582294042 , 4.67917911 , 0 ], [2.280362439 , 2.866990263 , 0 ], [7.423436942 , 4.696522875 , 1 ], [5.745051997 , 3.533989803 , 1 ], [9.172168622 , 2.511101045 , 1 ], [7.792783481 , 3.424088941 , 1 ], [7.939820817 , 0.791637231 , 1 ]] ''' 这里忽略了separate_by_class等其他函数,他们和前面的代码完全相同,没有修改 ''' def evaluate_algorithm (data_set, model, n_folds ): folds = kfold_split(data_set, n_folds) print (folds) scores = [] for fold in folds: train_set = list (folds) train_set.remove(fold) print ("fold" , fold) train_set = sum (train_set, []) print ("train_set" , train_set) test_set = [] for row in fold: row_copy = list (row) row_copy[-1 ] = None test_set.append(row_copy) print ("test_set" , test_set) predicted = model(train_set, test_set) actual = [row[-1 ] for row in fold] score = accuracy_score(actual, predicted) scores.append(score) return scores if __name__ == '__main__' : scores = evaluate_algorithm(data_set_demo, naive_bayes, n_folds=5 ) print ('Scores: %s' % scores) print ('Mean Accuracy: %.3f' % mean(scores))
打印的日志如下:很明显可以看出被kfold分为的5组数据里面有4组数据具有相同的label值,这样会影响训练效果。因此有必要使用StratifiedKFold算法进行改进。
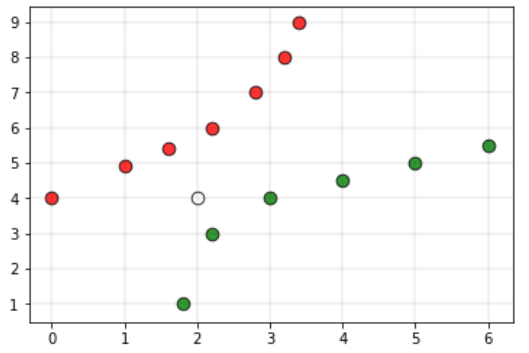
练习:KNN算法 可以参考上面iris代码的具体实现,按下列流程实现算法:
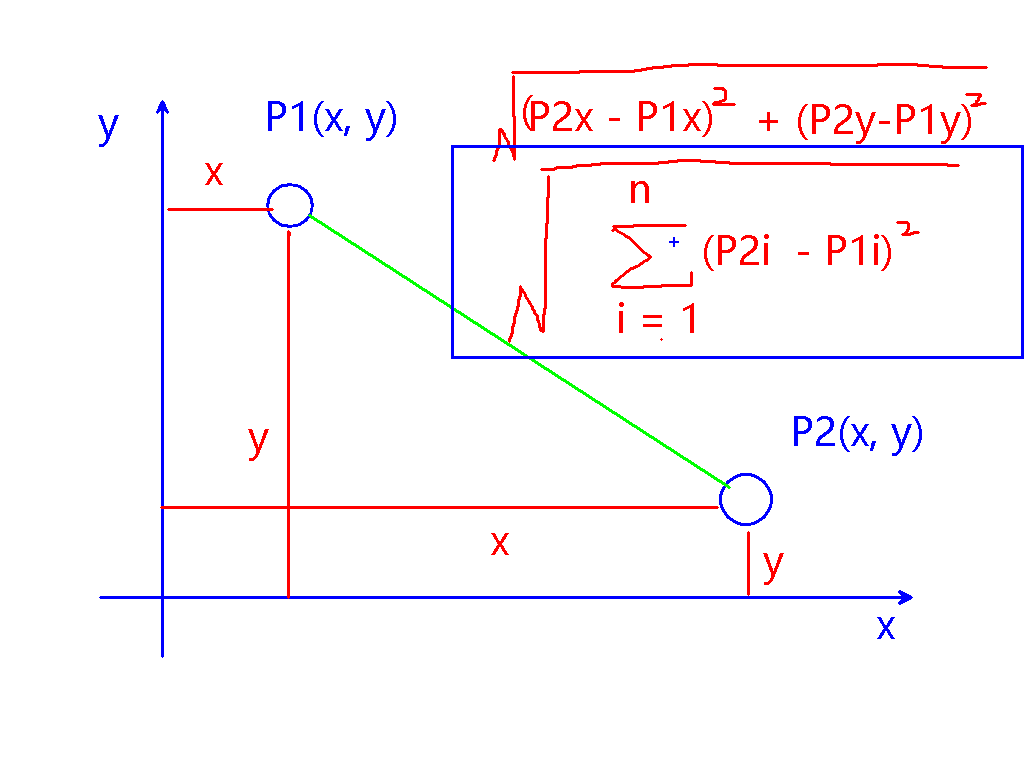
1 - 计算欧几里得距离;
使用如下欧几里得距离公式计算空间中2个点的坐标
其他
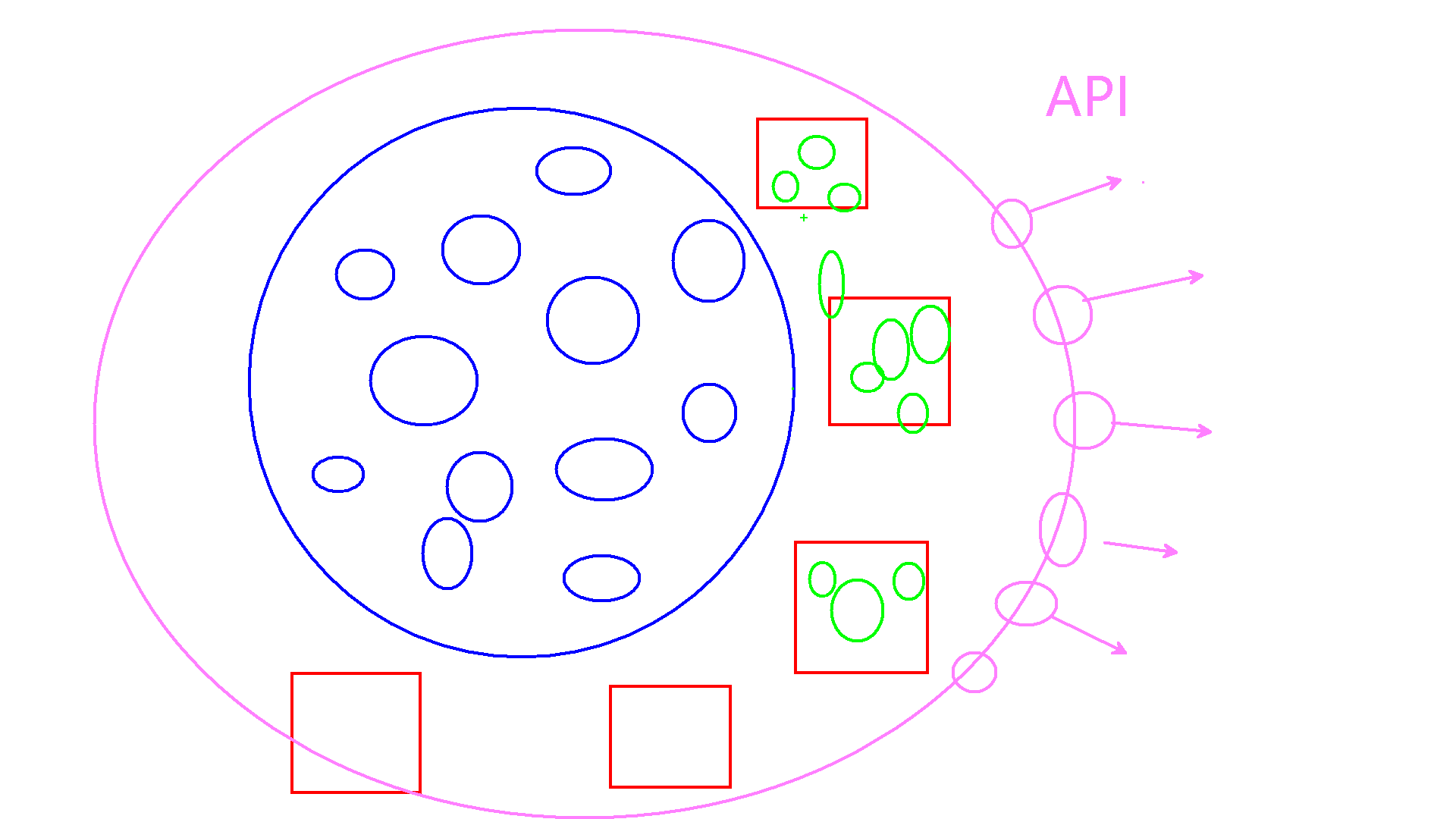
根据数据 训练模型 、然后对外提供使用的API ,即数据+应用的方式,例如ChatGPT的API。这样的产品依赖性更高,而且比传统的开发产品更有利润。开发人员也更轻松,主要负责算法即可,这是一种努力的方向。
目前能做的是绿色部分,为后面做准备。
参考scikit-learn官方文档 ,里面的原理写的很详细,了解后把里面的算法自己写代码实现。
不要被外物(第三方库、框架等)干扰,多修炼内功(算法、数学等)。